6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais
6.4.4.6. Identificação do Modelo de Box-Jenkins
6.4.4.6.2. |
Identificação do modelo para os dados de concentrações de CO2 |
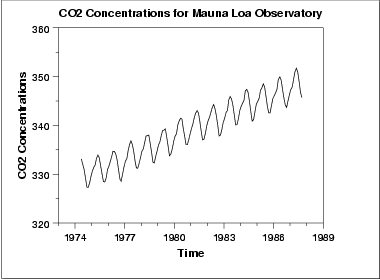
O gráfico inicial run sequence dos dados indica uma tendência de subida. Uma inspeção visual deste gráfico indica que um ajuste linear simples deverá ser suficiente para remover esta tendência para cima.
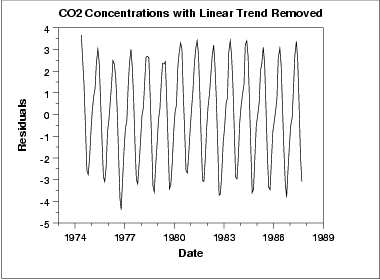
Este gráfico contém os resíduos do ajuste linear aos dados originais. Depois da remoção da tendência linear, o gráfico run sequence indica que os dados têm uma localização constante e variância, que implicam numa estacionariedade.
Entretanto, o gráfico mostra sazonalidade. Geramos um gráfico de autocorrelação para ajudar determinar o período seguido pelo gráfico da subsérie sazonal.
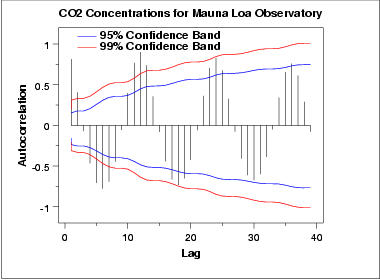
O gráfico de autocorrelação mostra um padrão alternativo de estacas positivas e negativas. Ele mostra também um padrão repetitivo a cada 12 lags, que indica um efeito de sazonalidade.
As duas linhas conectadas no gráfico de autocorrelação são os intervalos de confiança de 95% e 99% para a significância estatística das autocorrelações.
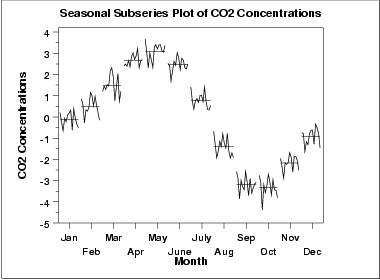
Um padrão de sazonalidade significativa é óbvio neste gráfico, de modo que precisamos incluir termos sazonais no ajustamento de um modelo de Box-Jenkins. Como estes são dados mensais, geralmente incluiríamos termos autoregressivos sazonais de 12 lags e/ou média móvel.
Para ajudar identificar componentes não sazonais, tomaremos uma diferença sazonal de 12 e geraremos o gráfico de autocorrelação nos dados diferenciados na sazonalidade.
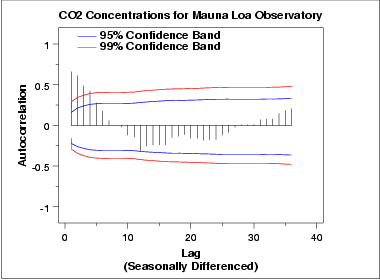
Este gráfico de autocorrelçao mostra uma mistura de decaimento exponencial e um padrão senoidal amortecido. Isto indica que um modelo AR, com ordem superior a um, pode ser apropriado. Geramos um gráfico de autocorrelação para ajudar identificar a ordem.
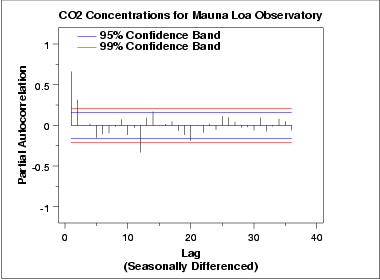
O gráfico de autocorrelação parcial sugere que um modelo AR(2) poderá ser apropriado desde que a autocorrelação parcial torna-se zero após o segundo lag. O lag 12 é também significativo, indicando alguma sazonalidade remanescente.
Em resumo, nossa tentativa inicial será ajustar um modelo AR(2) com um termo AR(12) sazonal nos dados com uma tendência linear removida. Poderíamos tentar o modelo com e sem diferenciação sazonal aplicada. A validação do modelo deverá ser realizada antes de aceitar este como um modelo final.

