6.
Controle e Monitoramento de Produto ou Processo
6.4.
Introdução à Analise de Séries Temporais
6.4.4.
Modelos Univariados de Séries Temporais
6.4.4.6.
|
Identificação do Modelo de Box-Jenkins
|
|
|
Estacionariedade e Sazonalidade
|
O primeiro passo no desenvolvimento de um modelo de Box-Jenkins é determinar se a série é estacionária e se existe qualquer sazonalidade significativa que precisa ser modeladda.
|
|
Detectando Estacionariedade
|
A estacionariedade pode ser avaliada de um gráfico de sequência de execução.
O gráfico de sequência de execução deverá se mostrar constante em localização e escala.
Ela pode também ser detectada de um gráfico de autocorrelação.
Especificamente, a não estacionariedade é frequentemente indicada por um gráfico de autocorrelação com um decaimento muito lento.
|
|
Detectando sazonalidadae
|
Sazonalidade (ou periodicidade) pode ser geralmente estimada de umgráfico de autocorrelação, um gráfico da subsérie sazonal, ou
um gráfico espectral.
|
|
Diferenciação para se atingir a estacionariedade
|
Box and Jenkins recomendaram a abordagem de diferenciação para se atingir a estacionariedade. Entretanto, ajustar uma curva e subtrair os valores ajustados dos dados originais pode também ser usado no contexto dos modelos de Box-Jenkins.
|
|
Diferenciação sazonal
|
No estágio de identificação do modelo, nossa meta é detectar sazonalidade, se existir, e identificar a ordem dos termos de média móvel sazonal e dos termos autoregressivos. Para muitas séries,
o período é conhecido e um único termo de sazonalidade é suficiente.
Por exemplo, para dados mensais tipicamente incluiríamos um termo AR 12 sazonal ou um termo MA 12 sazonal. Para modelos Box-Jenkins, não removemos explicitamente a sazonalidadae antes de ajustar o modelo. Em vez disso, incluímos a ordem dos termos sazonais na especificação do modelo apara a estimação do software ARIMA. Entretanto,
pode ser útil aplicar uma diferença sazonal aos dados e gerar novamente os gráficos de autocorrelação parcial e autocorrelação.
Isto pde ser útil na identificação do componente não sazonal do modelo. Em alguns casos, a diferenciação sazonal pode remover a maioria ou todos os efeitos de sazonalidade.
|
|
Identificar p e q
|
Uma vez a estacionariedade e a sazonalidade ter sido endereçada, o próximo passo é identificar a ordem (i.e., o p e
q) das partes autoregressiva e média móvel.
terms.
|
|
Gráficos de Autocorrelação e Autocorrelação Parcial
|
A principal feramenta para se fazer isto é o
gráfico de autocorrelação
e o gráfico de autocorrelação parcial.
A amostra do gráfico de autocorrelação e a amostra do gráfico de autocorrelação parcial são comparados ao comportamento teórico destes gráficos quando a ordem é conhecida.
|
| Ordem do Processo Autoregressivo (p) |
Especificamente, para um processo AR(1), a sample função autocorrelação deverá ter uma aparência de decréscimo exponencial.
Entretanto, processos AR de ordem superior são frequantemente uma mistura de componentes decrescimento exponencial e senoidal amortecido.
Para processos autoregressivos de ordem superior, a autocorrelação da amostra precisa ser suplementada com um gráfico de autocorrelação parcial. A autocorrelação parcial de um processo
AR(p) torna-se zero no lag p+1
e superiores, assim examinamos a função autocorrelação parcial da amostra para ver se existe evidência de um desvio do zero. Isto é geralmente determinado colocando um intervalo de confiança de 95% no gráfico de autocorrelação parcial da amostra(a maioria dos most softwares que geram gráficos de autocorrelação de amostras plotarão também este intervalo de confiança). Se o software não gerar a banda de confiança, ela é aproximadamente 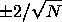 ,
com N denotando o tamanho da amostra. ,
com N denotando o tamanho da amostra.
|
|
Ordem do Processo de Média Móvel (q)
|
A função autocorrelação de um processo MA(q) torna-se zero no lag q+1 e superiores,
então examinamos a função autocorrelação da amostra para ver onde ela essencialmente torna-se zero. Fazemos isto colocando o intervalo de confiança de 95% para a função autocorrelação da amostra no gráfico de autocorrelação da amostra. A maioria dos softwares que pode gerar o gráfico de autocorrelação poded também gerar este intervalo de confiança.
A função autocorrelação parcial da amostra não é geralmente útil para identificar a ordem do processo de média móvel.
|
|
Forma da Função Autocorrelação
|
A tabela seguinte resume como usamos a função autocorrelação da amostra para identificação do modelo.
|
FORMA
|
MODELO INDICADO
|
|
Exponential, decaindo a zero
|
Modelo autoregressivo. Use o gráfico de autocorrelação parcial
para identificar a ordem do modelo autoregressivo.
|
|
Alternando positivo and negativo, decaindo a zero
|
Modelo autoregressivo. Use o gráfico de autocorrelação parcial
para ajudar identificar a ordem.
|
|
Uma ou mais estacas, restante é essencialmente zero
|
Modelo média móvel, ordem identificada por onde o gráfico torna-se zero.
|
|
Decai, iniciando após poucos lags
|
Modelo autoregressivo misturado e média móvel.
|
|
Tudo zero ou próximo de zero
|
Os dados são essencialmente aleatórios.
|
|
Valores altos nos intervalos fixaados
|
Inclui o termo autoregressivo sazonal.
|
|
Não decai a zero
|
A série não é estacionária.
|
|
|
Modelos Mistos Dificultam a Identificação
|
Na prática, as funções autocorrelação e autocorrelação parcial da amostra são variáveis aleatórias e não darão o mesmo quadro que as funções teóricas. TIsto torna a identificação do modelo mais difícil. Em particular, modelos mistos podem ser particularmente difícieis de se identificar.
Embora a experiência seja útil, desenvolver bons modelos usando estes gráficos amostrais pode causar muitas tentativas e erros. Por esta razão, critérios baseados em informações de anos recentes tais como FPE (Final Prediction Error) e AIC
(Aikake Information Criterion) e outros tem sido preferidos e usados.
Estas técnicas podem ajudar automatizar o processo de identificação do modelo. Estas técnicas requerem softwares computacionais a serem usados. Felizmente, estas técnicas estão disponíveis em muitos softwares estatísticos comerciais que fornecem as capacidades de modelagem ARIMA.
Para informação adicional destas técnicas, ver
Brockwell e Davis (1987,
2002).
|
|
Exemplos
|
Mostramos uma série típica de gráficos para realizar a identificação do modelo inicial para
- os dados de oscilações do sul e
- os dados de concentrações mensais de CO2
.
|
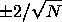 ,
com N denotando o tamanho da amostra.
,
com N denotando o tamanho da amostra.

