6.
Controle e Monitoramento de Produto ou Processo
6.4.
Introdução à Analise de Séries Temporais
6.4.3.
O que é Suavização Exponencial?
6.4.3.3.
|
Suavização Exponencial Dupla
|
|
|
A suavização exponencial dupla usa duas constantes e é melhor para se manipular tendências
|
Como foi observado anteriormente, a Suavização Simples não é excelente para seguir os dados quando houver tendência. Esta situação pode ser melhorada pela introdução de uma segunda equação com uma segunda constante,
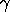 , que deve ser escolhida conjuntamente com , que deve ser escolhida conjuntamente com  . .
Aqui estão as duas equações associadas com a Suavização Exponencial Dupla:
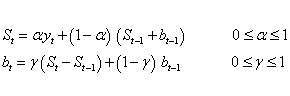 Note que o valor atual da série foi usado para calcular seu valor suavizado trocado na suavização exponencial.
Note que o valor atual da série foi usado para calcular seu valor suavizado trocado na suavização exponencial.
|
|
|
Valores Iniciais
|
|
Vários métodos para se escolher os valores iniciais
|
Como no caso da suavização simples, existem uma variedade de esquemas para definir os valores iniciais para St e
bt na suavização dupla.
S1 é em geral definido como y1. Aqui estão três sugestões para b1:
|
|
|
Comentários
|
|
Significado das equações de suavização
|
A primeira equação de suavização ajusta St diretamente
para a tendência do período anterior, bt-1,
adicionando-a ao último valor suavizado, St-1.
Isto ajuda eleiminar o lag e leva St à base apropriada do valor atual.
A segunda equação de suavização atualiza então a tendência, que é expressa como a diferença entre os dois últimos valores. A equação é similar à forma básica da suavização simples, mas aqui aplicada à atualização da tendência.
|
|
Técniccas de otimização não lineares podems ser usadas
|
Os valores para
 e e
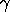 podem ser obtidos via técnicas de otimização não lineares, tais como o Algirítmo de Marquardt.
podem ser obtidos via técnicas de otimização não lineares, tais como o Algirítmo de Marquardt.
|
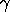 , que deve ser escolhida conjuntamente com
, que deve ser escolhida conjuntamente com  .
.
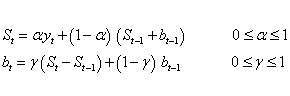
 e
e
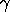 podem ser obtidos via técnicas de otimização não lineares, tais como o Algirítmo de Marquardt.
podem ser obtidos via técnicas de otimização não lineares, tais como o Algirítmo de Marquardt.

