6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais
6.4.5.1. |
Exemplo de Análise de Séries Temporais Multivariadas |
-
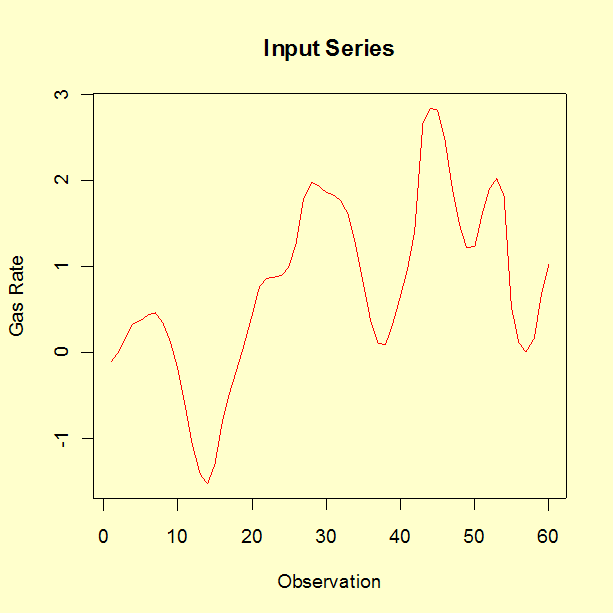
Entrada do Gás Metano Inflamável = 0.60 - 0.04 X(t)
 /ul>
/ul>
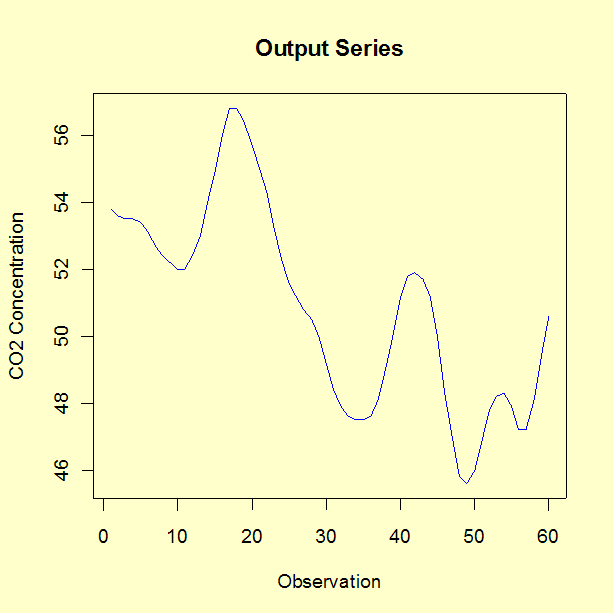
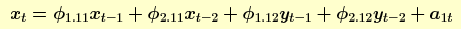
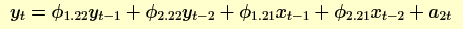
As estimativas do parâmetro para a equação associada com a taxa de gás são os seguintes.
Estimativa Erro Padrão t valor Pr(>|t|)
a1t 0.003063 0.035769 0.086 0.932
φ1.11 1.683225 0.123128 13.671 < 2e-16
φ2.11 -0.860205 0.165886 -5.186 3.44e-06
φ1.12 -0.076224 0.096947 -0.786 0.435
φ2.12 0.044774 0.082285 0.544 0.589
Erro padrão residual: 0.2654 baseado em 53 graus de liberdade
R-quadrado múltiplo: 0.9387
R-quadrado ajustado: 0.9341
F-estático: 203.1 baseado em 4 e 53 graus de liberdade
p-value: < 2.2e-16
As estimativas do parâmetro para a equação associada com a concentração de CO2 são as seguintes.
Estimativa Erro Padrão t value Pr(>|t|)
a2t -0.03372 0.01615 -2.088 0.041641
φ1.22 1.22630 0.04378 28.013 < 2e-16
φ2.22 -0.40927 0.03716 -11.015 2.57e-15
φ1.21 0.22898 0.05560 4.118 0.000134
φ2.21 -0.80532 0.07491 -10.751 6.29e-15
Erro padrão residual: 0.1198 baseado em 53 graus de liberdade
R-quadrado múltiplo: 0.9985
R-quadrado ajustado: 0.9984
F-estático: 8978 baseado em 4 e 53 graus de liberdade
p-value: < 2.2e-16
Testes de Box-Ljung realizados para cada série para testar a aleatoriedade dos 24 primeiros resíduos não foram significativos. Os p-values para os testes usando concentração CO2 residuais e taxa de gás residual foram 0.4 e 0.6, respectivamente.
O método de previsão é uma extensão do modelo e segue a teoria delineada na seção anterior. Os valores previstos das próximas seis observações (61-66) e os limites de confiança de 90% associados estão mostrados abaixo para cada série.
Limite 90% Concentração Limite 90%
Observação Inferior Prevista Superior
----------- --------- -------- ---------
61 51.0 51.2 51.4
62 51.0 51.3 51.6
63 50.6 51.0 51.4
64 49.8 50.5 51.1
65 48.7 50.0 51.3
66 47.6 49.7 51.8
Limite 90% Taxa Limite 90%
Observation Inferior Prevista Superior
----------- --------- -------- ---------
61 0.795 1.231 1.668
62 0.439 1.295 2.150
63 0.032 1.242 2.452
64 -0.332 1.128 2.588
65 -0.605 1.005 2.614
66 -0.776 0.908 2.593

