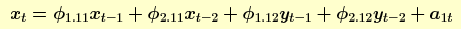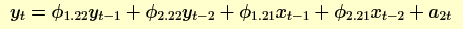6. Controle e Monitoramento de Produto ou Processo
6.4. Introdução à Analise de Séries Temporais
6.4.5. Modelos de Séries Temporais Multivariadas
|
|
Se cada observação série temporal é um vetor de números, você pode modelar a mesma usando uma forma multivariada do modelo Box-Jenkins
|
A forma multivariada dos modelos univariados de Box-Jenkins é algumas vezes chamada de modelo ARMAV, para o processo AutoRegressive Moving Average
Vector ou simplesmente processo ARMA vetorial.
O modelo ARMAV para uma stationary série temporal multivariada ,
com uma média vetorial zero, representado por
é da forma
onde
Como um exemplo, para uma série bivariada com n = 2,
p = 2, e q = 1, o modelo ARMAV(2,1) é:
with
|
|
Dificuldade na estimação dos parâmetros e matriz covariância
|
A estimação dos parâmetros matriciais e matriz covariância é complicado e muito difícil sem um software computacional. A estimação das matrizes de Média Móvel é especialmente uma experiência difícil. Se optarmos por ignorar a(s) componente(s) MA ficamos com o modelo ARV dado por:
onde
Um modelo com p parâmetros matriciais autoregressivos é um modelo ARV(p) ou um modelo vetorial AR.
Os parâmetros matriciais podem ser estimados pelos mínimos quadráticos multivariados,
mas existem outros métodos tais como a estimação máxima verosimilhança.
|
|
Propriedades interessantes dos parâmetros matriciais
|
Existem uma poucas propriedades interessantes associadas com o phi ou parâmetros matriciais AR. Considere o seguintge exemplo para uma série bivariada com n =2, p = 2, e q = 0. O modelo ARMAV(2,0)
é:
|
|
|
Sem perda de generalidade, assuma que a série X seja entrada e a série Y seja saída e o vetor média = (0,0).
Portanto, tranforme a observação subtraindo suas médias respectivas.
|
|
Termos diagonais da matriz Phi
|
Os termos diagonais de cada matriz Phi são estimativas escalares para cada série, neste caso:
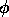 1.11, 1.11,
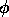 2.11
para a série de entrada X, 2.11
para a série de entrada X,
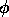 1.22, 1.22,
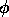 .2.22
para a série de saída Y. .2.22
para a série de saída Y.
|
|
Mecanismo de transferência
|
Os elementos inferiores fora da diagonal representam a influência da entrada na saída.
Isto é chamado de mecanismo de "transferência" ou modelo função transferência como discutido por Box e Jenkins no Capítulo 11. Os termos 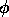 aqui correspondem aos seus termos aqui correspondem aos seus termos 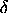 . .
Os termos superiores fora da diagonal representam a influência da saída na entrada.
|
|
Feedback
|
Isto é chamado de "feedback". A presença de feedback pode também ser vista como um alto valor para um coeficiente na matriz de correlação dos resíduos. Um modelo de transferência "verdadeiro" existe quando não há feedback.
Isto pde ser visto expressando a forma matricial na forma escalar:
|
|
Retardo
|
Finalmente, retardo ou tempo de "inatividade' pode ser medido estudando os elementos inferiores fora da diagonal novamente.
Se, por exemplo,
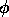 1.21
não for significativo, o retardo é 1 período de tempo. 1.21
não for significativo, o retardo é 1 período de tempo.
|
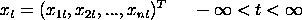
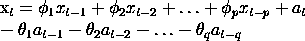

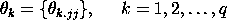
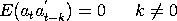
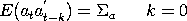
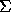 a
é a dispersão ou matriz covariância de at
a
é a dispersão ou matriz covariância de at
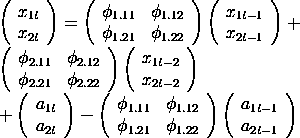
![a(t) = [a(1t); a(2t)]](eqns/at.gif)
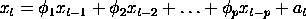

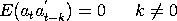
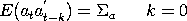

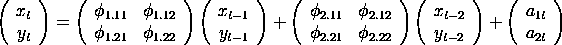
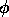 1.11,
1.11,
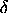 .
.