6.
Controle e Monitoramento de Produto ou Processo
6.4.
Introdução à Analise de Séries Temporais
6.4.3.
O que é Suavização Exponencial?
6.4.3.1.
|
Suavização exponencial Simples
|
|
|
A suavização exponencial simples pondera as observações passadas com pesos decrescentes exponencialmente para previsão de valores futuros
|
Este esquema de suavização começa definido S2 para
y1, onde Si representa a observação suavizada ou EWMA, e y representa a observação original.
Os subscritos se referem aos períodos de tempo, 1, 2, ..., n. Para o terceiro período, S3 =
 y2 +
(1-
y2 +
(1- )
S2; e assim por diante. Não há S1;
a série suavizada inicia com a versão suavizada da segunda observação. )
S2; e assim por diante. Não há S1;
a série suavizada inicia com a versão suavizada da segunda observação.
Para qualquer período de tempo t, o valor suavizado St
é encontrado calculando
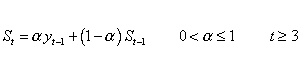 Esta é a equação básica da suavização exponencial e a constante ou parâmetro
Esta é a equação básica da suavização exponencial e a constante ou parâmetro
 é chamado de constante de suavização.
é chamado de constante de suavização.
Nota: Existe uma abordagem alternativa para suavização exponencial que troca yt-1 na equação básica com yt, a observação atual. Esta formulação,
devida a Roberts (1959), é descrita na seção sobre Gráficos de controle EWMA. A formulação aqui segue Hunter (1986).
|
|
|
Definindo o primeiro EWMA
|
|
A primeira previsão é muito importante
|
O EWMA inicial faz um importante papel no cálculo de todos os EWMA's subsequentes. Definindo S2 como
y1 é um método de inicialização. Outra maneira é defini-lo como alvo do processo.
Ainda outra possibilidade seria fazer a média das quatro ou cinco primeiras observações.
Pode ser mostrado que o menor valor de  , o mais importante é a seleção do EWMA inicial. O usuário deveria ser orientado para tentar uns poucos métodos, (assumindo que o software está disponibilizado) antes da finalização das definições. , o mais importante é a seleção do EWMA inicial. O usuário deveria ser orientado para tentar uns poucos métodos, (assumindo que o software está disponibilizado) antes da finalização das definições.
|
|
|
Por que é chamada "Exponencial"?
|
|
Expandindo a equação básica
|
Vamos expandir a equação básica primiero substituindo St-1 na equação básica para obter
St =
 yt-1 +
(1-
yt-1 +
(1- )
[ )
[  yt-2 +
(1-
yt-2 +
(1- )
St-2 ] )
St-2 ]
=
 yt-1 +
yt-1 +
 (1-
(1- )
yt-2 +
(1- )
yt-2 +
(1- )2
St-2 )2
St-2
|
|
Fórmula de somatório para a equação básica
|
Substituindo por St-2, depois então por
St-3, e assim por diante, até atingirmos
S2 (que é exatamente y1), pode ser mostrado que a equação expandida pode ser escrita como:
![S(t) = alpha*SUM[i=0 to t-2][(1-alpha)**(i-1)*y(t-1)] +
(1-alpha)**(t-2)*S(2), t >= 2](eqns/ts11acor.gif)
|
|
Equação expandida para S5
|
POr exemplo, a equação expandida para o valor suavizado
S5 é:
![S(5) = alpha*[(1-alpha)**0*y(5-1) + (1-alpha)**1*y(5-2) +
(1-alpha)**2*y(5-3)] + (1 - alpha)**3*S(2)](eqns/ts12.gif)
|
 y2 +
(1-
y2 +
(1- )
S2; e assim por diante. Não há S1;
a série suavizada inicia com a versão suavizada da segunda observação.
)
S2; e assim por diante. Não há S1;
a série suavizada inicia com a versão suavizada da segunda observação.
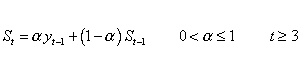
 é chamado de constante de suavização.
é chamado de constante de suavização.
 , o mais importante é a seleção do EWMA inicial. O usuário deveria ser orientado para tentar uns poucos métodos, (assumindo que o software está disponibilizado) antes da finalização das definições.
, o mais importante é a seleção do EWMA inicial. O usuário deveria ser orientado para tentar uns poucos métodos, (assumindo que o software está disponibilizado) antes da finalização das definições.
 yt-1 +
(1-
yt-1 +
(1- )
[
)
[  yt-2 +
(1-
yt-2 +
(1- )
St-2 ]
)
St-2 ]
 yt-1 +
yt-1 +
 (1-
(1- )
yt-2 +
(1-
)
yt-2 +
(1- )2
St-2
)2
St-2
![S(t) = alpha*SUM[i=0 to t-2][(1-alpha)**(i-1)*y(t-1)] +
(1-alpha)**(t-2)*S(2), t >= 2](eqns/ts11acor.gif)
![S(5) = alpha*[(1-alpha)**0*y(5-1) + (1-alpha)**1*y(5-2) +
(1-alpha)**2*y(5-3)] + (1 - alpha)**3*S(2)](eqns/ts12.gif)

**i =
alpha*[(1 - (1-alpha)**t)/(1 - (1-alpha))] = 1 - (1-alpha)**t](eqns/ts10.gif)
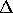 and
and