Séries Temporais no Python

Volta ao Menu Principal

As séries temporais são usadas para fazermos previsões. Uma visão geral sobre metodologia de previsão pode ser encontrada no site do Prof. Bertolo na área de Métodos QuantitativosClique aqui. Temos também uma apostila bem completa tratando de Métodos Básicos de Previsão no Excel Clique aqui.

A maioria dos dados financeiros estão em séries temporais. Esta é a razão do porque enfatizamos nas análises de datas e configuramos as datas como índices. Quando operamos com dados de séries temporais, frequentemente temos de redimensiona-los em diferentes frequências, tais como de diariamente para mensalmente. O Pandas tem métodos embutidos para tratar com esses exercícios de redimensionamentos.

Para ilustrar o ponto de redimensionamento, vou baixar os preços diários da GOLL4.SA do Yahoo! Finance^R para o mesmo período. O nome do arquivo que armazenei no meso diretório dessa notebook Jupyter tem extensãocsv, assim GOLL4_c.csv.

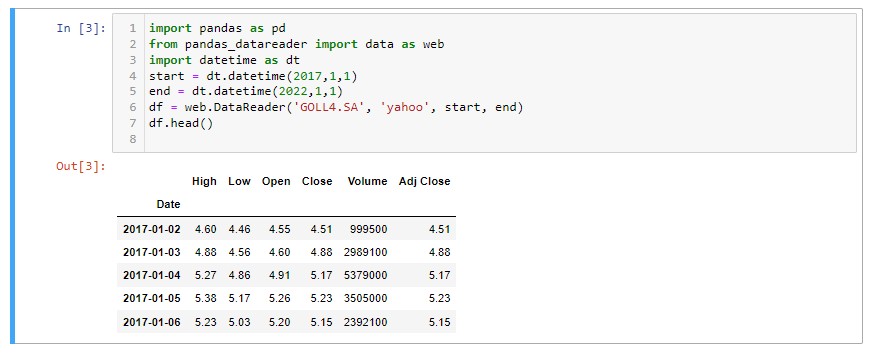
Agora vamos criar o DataFrame baixando o arquivo diretamente do Yahoo GOLL4.SA:

Agora vamos imprimir as 5 primeiras linhas do arquivo acima GOLL4.SAarmazenado no nosso diretório como GOL.csv:

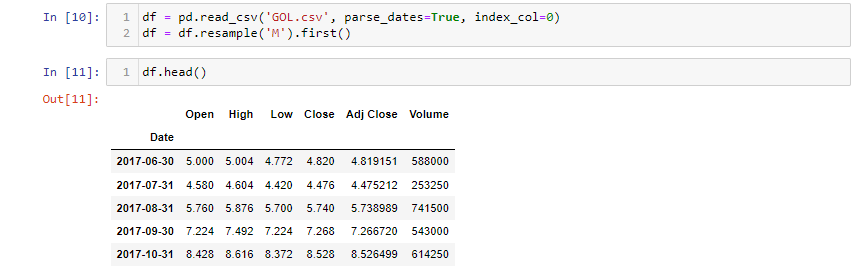
O parâmetro em .resample() é para a frequência desejada dos dados. Aqui está uma lista para tais frequências: “A”: anual “Q”: trimestral “M”: mensal “W”: semanal “D”: diária “H”: horária “T”: por minuto “S”: por segundo

O método secundário .last() é para dizer ao Pandas para usar a última data de negociação do mês como o preço mensal. Se .first() for usada, o primeiro ponto de dados do mês será usado. Mas esta diferença de amostragem é que causa confusão. Se você observar os dados mensalmente do Yahoo! Finance^R, mostrados no começo deste capítulo, e aquele que aquele que acabamos de redimensionar dos dados diários. Existem diferenças óbvias. A razão é que o Yahoo! Finance^R converte diariamente para mensalmente escolhendo a última data de negociação do mês, mas mostra como o primeiro dia do mês. Assim os rótulos de data não estão corretos no Yahoo! Finance^R.

Mas se nós reamostramos ela por nós mesmos dos dados diários, ela somente estará correta se usarmos .last(). Se redimensionarmos com .first(), o Pandas colherá os dados da primeira data de negociação do mês, mas o índice coluna, mostrará a data do final do mês. Essa é uma peculiaridade envolvida na reamostragem. A única maneira de não ficar confuso é olhar para os dados diários originais.

Você pode também usar .mean() para fazer uma média simples dos preços diários, mas isto é geralmente desencorajador em análise de séries temporais para o potencial problema de correlação serial.

Vamos agora traçar um gráfico de linha simples para esta série temporal:

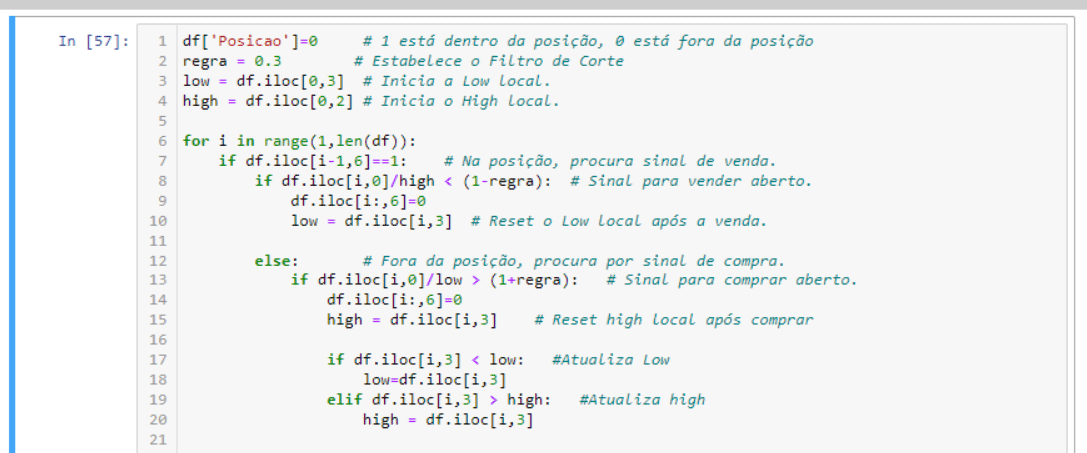
Aqui traçamos os dados da coluna "Volume".

Agora vamos plotar todas as outras colunas usando subplot:

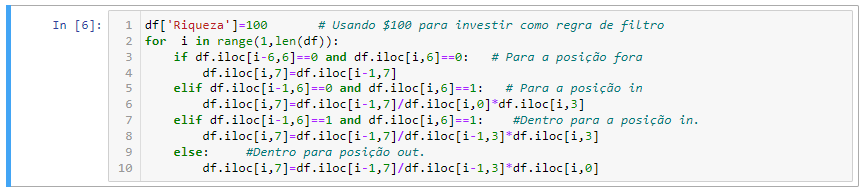
Os gráficos de linha usados acima mostram a sazonalidade Clique aqui, que, em séries temporais, é a presença de variações que ocorrem em intervalos de tempo regulares específicos inferiores a um ano, por exemplo, semanal, mensal, trimestral.

Outro conceito importante é a reamostragem que é uma metodologia de uso econômico de uma amostra de dados para melhorar a precisão e quantificar a incerteza de um parâmetro populacional. Reamostrar por meses ou semanas e fazer gráficos de barra é outro método muito simples e amplamente usado para encontrar a sazonalidade. Aqui, vamos fazer um gráfico de barras com dados mensais.

Outro conceito é a diferenciação que é usada para fazer a diferença nos valores de um intervalo especificado. Por padrão, é um, podemos especificar valores diferentes para gráficos. É o método mais popular para remover tendências nos dados:

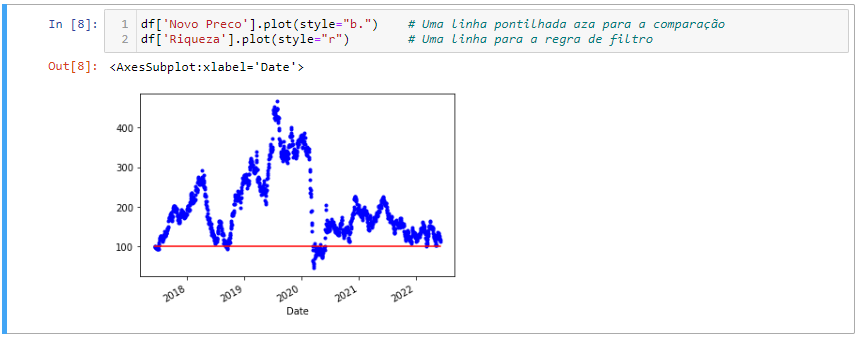
Plotando as mudanças nos dados

Também podemos representar graficamente as mudanças que ocorreram nos dados ao longo do tempo. Existem algumas maneiras de representar graficamente as alterações nos dados.

Shift - A função shift pode ser usada para deslocar os dados antes ou depois do intervalo de tempo especificado. Podemos especificar a hora e, por padrão, ele mudará os dados em um dia. Isso significa que obteremos os dados do dia anterior. É útil ver os dados do dia anterior e os dados de hoje simultaneamente, lado a lado.

No código acima, a função .div() ajuda a preencher os valores de dados ausentes. Na verdade, div() significa divisão. Se tomarmos data. div (6) dividirá cada elemento em data por 6. Fazemos isso para evitar os valores nulos ou ausentes que são criados pela operação 'shift()'.

Aqui, pegamos .div (data.Close.shift()), ele dividirá cada valor de data em data.Close.shift() para remover os valores nulos.

Também podemos pegar um intervalo específico de tempo e traçar para ter uma visão mais clara. Aqui, estamos plotando os dados de apenas 2021.

Ajuste e Modelos de Série Temporal

Para uma visão teórica bem profunda sobre análise de séries temporais recomendamos o site do Prof. Bertolo

A maioria dos dados financeiros são séries temporais. Ajustar dados financeiros com modelos de séries temporais para entender os dados é prática comum do setor. O Python tem um monte de funções embutidas para cuidar dos modelos de séries temporais.

Um Modelo AutoRegressivo (AR) com statsmodels.tsa

Vamos ilustrar como estimar com modelos de séries temporais com um modelo autorregressivo simples, com um período de atraso. O assim chamdo Modelo AR(1) pode ser escrito como:

Nosso exemplo ainda é baseado nos registros diários da GOLL4.SA.

Tentemos o seguinte código:

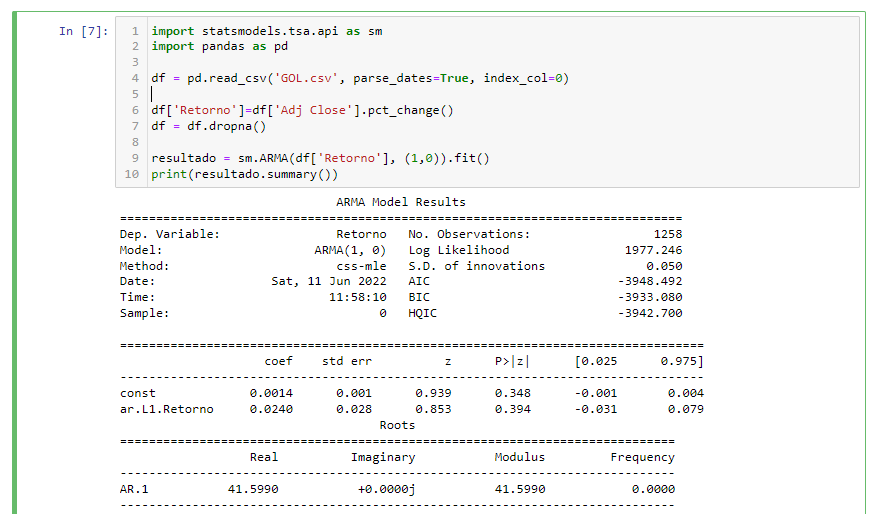
Note que o processo AR é parte de um modelo ARMA (AutoRegressive Moving Average) maior na família. Estimar com um modelo AR(1) é a mesma coisa que estimar com um modelo ARMA com um polinomial AR atrasado de 1 e atraso no MA na linha 7. Para séries de dados e fitted com ARMA(p,q), a função é chamada de sm.ARMA(y,(p,q)).

Não é surpresa que a série de retornos da ação não siga um modelo autorregressivo simples. O coeficiente do termo atraso (lag) não é estatisticamente significativo. Apenas imagine quantos traders teriam empilhados destes achados, se eles fossem estatisticamente significativos. Mas ele serve para propósitos de nos ajudar no entendimento de ajuste ao modelo de séries temporais.

Funções de Autocorrelação

Mas seguimos adiante por nós mesmos. Para sérios ajustes com modelo de séries temporais, precisamos verificar a estacionariedade dos primeiros dados. O significado estatístico de estacionariedade pode ser entendido como dados tendo um equilíbrio de longo prazo no seu nível e volatilidade. A regressão de dados não estacionários pode somente encontrar uma relação espúria que tem pouca importância na interpretação.

Os preços de ações são geralmente acreditados serem não estacionários. Mas após tomarmos diferenças de preços para criar série de retorno, transformamos dados não estacionários e estacionários.

Existem várias maneiras de se verificar a estacionariedade. As funções de autocorrelação (ACF) que introduziremos são uma delas.

Para séries univariadas y_t, a correlação ρ entre duas observações, separadas por períodos s, podem ser escritas em função de s. Para uma série estacionária, quanto mais longe no tempo de dois y´s, menor a autocorrelação. No entanto, um ACF decaindo que converge a zero, geometricamente indica estacionariedade dos dados.

A biblioteca statsmodels tem uma função embutida sm.acf() que pode calcular o ACF de qualquer série univariada. Vamos usar os registros diários da GOL como um exemplo:

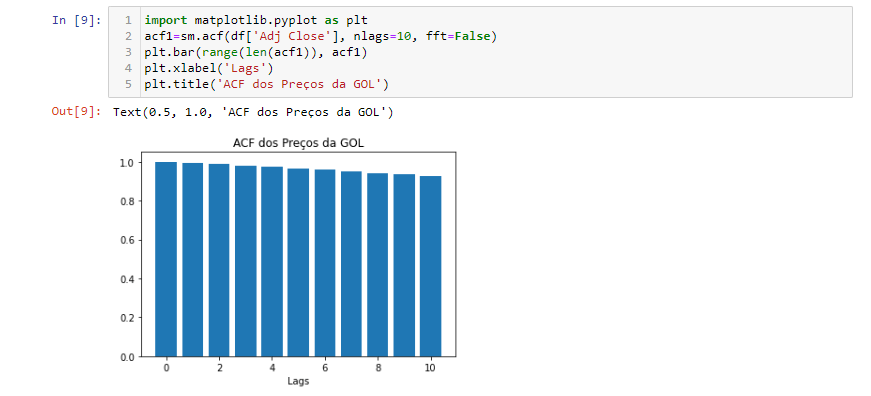
Como podemos ver no gráfico ACF, a autocorrelação não parece decair muito quando o número de lags aumentar. Será uma estória diferente quando visualizarmos a série de retorno no próximo bloco de código:

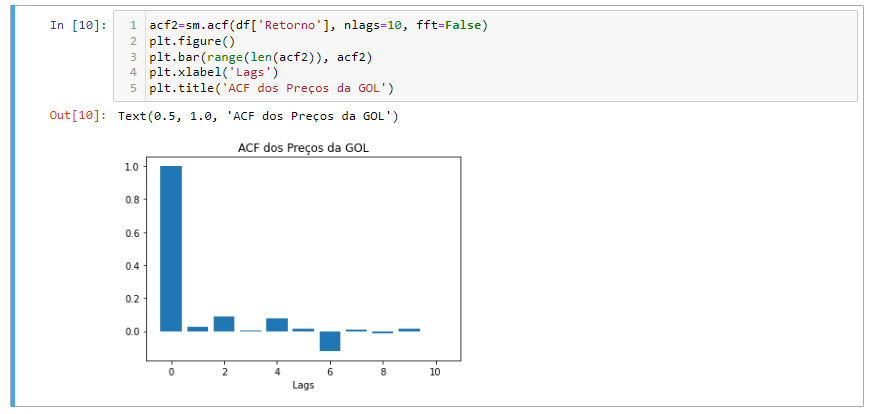
O decaimento acontece rápido. Não é ambíguo que a série de retorno pareça ser “mais estacionária” que a série de preços.

Teste de Dickey-Fuller aumentando para raiz unitária

O teste estacionário está frequentemente relacionado a uma importante hipótese em finanças: se o preço da ação seguir um processo random walk. A hipótese random walk é para descrever o movimento de um preço de ação da mesma maneira que um bêbado vagando à noite. O movimento do bêbado é totalmente randômico, mas se ele for empurrado numa certa direção, ele não resistirá. Em outras palavras, os preços são imprevisíveis, mas tem memória.

Se um processo de geração de dados for random walk, ele não é estacionário e também é sabido ter uma raiz unitária. Para testar se o processo tem uma raiz unitária, os pesquisadores, frequentemente, observam o seguinte modelo:

onde y_t é o nível de preços no instante t, o termo erro é referido como ruído ou inovação (vejam como os economistas misturam duas palavras ortogonais juntas) e a₀ é um termo a deriva (você pode pensa-lo como uma tendência natural dos preços das ações).

O coeficiente que estamos interessados nele é a₁, mas para tetar a hipótese da raiz unitária, frequentemente escrevemos a equação como:

Se y_t tiver uma raiz unitária, a₁ deverá não ser diferente de um e γ será zero. Em outras palavras, se não pudermos mostrar γ é estatisticamente diferente de zero, não podemos rejeitar a hipótese nula que y_t tem uma raiz unitária.

Este teste foi chamado de Dickey-Fuller (Dickey e Fuller, 1979).

A biblioteca statsmodels tem uma função embutida adfuller() para implementar o teste Dickey-Fuller. Vamos continuar com nosso exemplo GOL. Tente estas linhas.

O primeiro número é o teste estatístico. Comparando-o aos valores críticos de Dickey e Fuller (1979) (listado como um dic na saída, com 1%, 5% e 10%), encontramos que ele não é maior em valor absoluto que mesmo o 10%. Então sabemos que não podemos rejeitar a hipótese nula random walk. O segundo valor na saída é o p-value, que confirma a conclusão.

Tente usando a série de retorno da GOL para o teste Dickey-Fuller. Você deverá ser capaz de rejeitar a hipótese nula random walk sem qualquer dificuldade.

Quando uso a função sm.asfuller(), forneço somente dois parâmetros: a variável em questão e regressão = ‘c’. Este segundo argumento pode ser pego de um dict {‘c’, ‘ct’, ‘ctt’, ‘nc’}. Com somente ‘c’, estamos testando o modelo com uma deriva (drift). Se usamos ‘ct’, adicionamos uma tendência temporal ao modelo, em adição a deriva. Com registro diário em uso, não vejo um argumento forte para adicionar a tendência de tempo para o teste de hipótese.

Se você prestar atenção ao nome da função, você vê que ela é realmente chamada teste de Dickey-Fuller aumentado. Isto é para considerar a possível autocorrelação da série de dados. “Aumentamos” o modelo com variáveis lag. Especificamente, deveríamos testar:

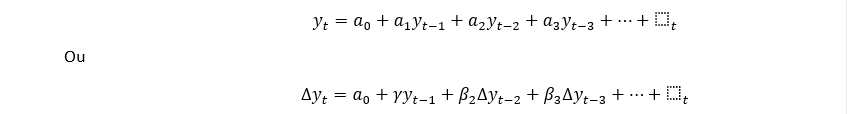
γ é ainda o coeficiente que estamos interessados nele. Frequentemente usamos ou AIC (Akaike Information Criterion) ou BIC (Bayesian Information Criterion) para selecionar o número de lags. Por exemplo,

O terceiro argumento em sm.adfuller() é escolher o método para selecionar o número de lags. Você pode tentar ‘AIC” ou ‘t-stat’ como uma alternativa. A saída diz que não podemos rejeitar a hipótese da raiz unitária.

ARIMA

Os fundamentos teóricos do que será tratado aqui pode sre encontrado no . Lá, também, pode ser encontrada uma apostila bem completa sobre Técnicas de Previsão de Box-Jenkins - ARIMA Clique aqui.

seção 17.4 do CHINA