Análises e Estatística no Objeto DataFrame

Volta ao Menu Principal

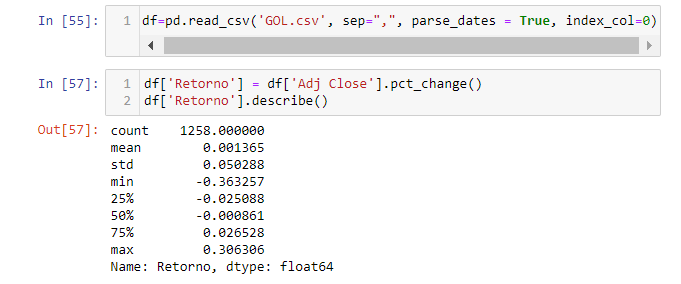
Quando pegamos em nossas mãos um dataset, sempre o visualizaremos primeiro plotando a série. Vamos deixar isso para depois e entraremos um pouco mais profuno nos números aqui observando seus resumos estatísticos que nos ajudarão analisá-los, juntamente, com os gráficos.s. Por exemplo:

Como está mostrado na saída, a GOLL4.SA, como uma ação, tem um retorno médio mensal positivo. Ele pode subir para um retorno de 30,6% num mês ou abaixar para -36,3%. Muitos dos números na tabela de resumos estatísticos podem ser extraídos diretamente. Por enquanto,

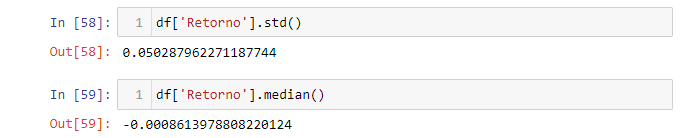
Para descobrir o valor de um percentil específico, você pode usar .quantile(). A linha seguinte dá a você a fatia de 95% dos valores da distribuição.

Média Móvel Simples

Os especuladores que seguem tendências geralmente analisam as médias móveis dos preços das ações. Uma média móvel é uma média aritmética dos preços de fechamento de vários dias de negociação consecutivos. Por exemplo, a média móvel de 50 dias é olhar para trás 50 dias de negociação primeiro. O criador de gráficos então soma todos os 50 preços de fechamento (Close) e divide a soma por 50.

Para uma visão teórica profunda sobre técnicas de suavização ou média móvel, recomendamos o site do Prof. Bertolo.

Podemos construir várias séries de médias móveis analisando várias quantidades de dias. Os populares são 20, 50, 100 e 250. Como as médias móveis suavizam a volatilidade de curto prazo, os traders podem identificar as tendências das ações com mais facilidade observando as médias móveis. Os sinais de negociação emergem dos cruzamentos de médias móveis variadas. Uma regra de negociação típica de média móvel simples (SMA) é comprar quando uma média móvel de curto prazo cruza uma de longo prazo por baixo. O cruzamento indica uma tendência ascendente. Torna-se um sinal de venda quando o curto prazo cruza o longo prazo de cima.

Vamos usar nossos preços diários da GOLL4.SA para criar médias móveis e ver se podemos detectar sinais de trading.

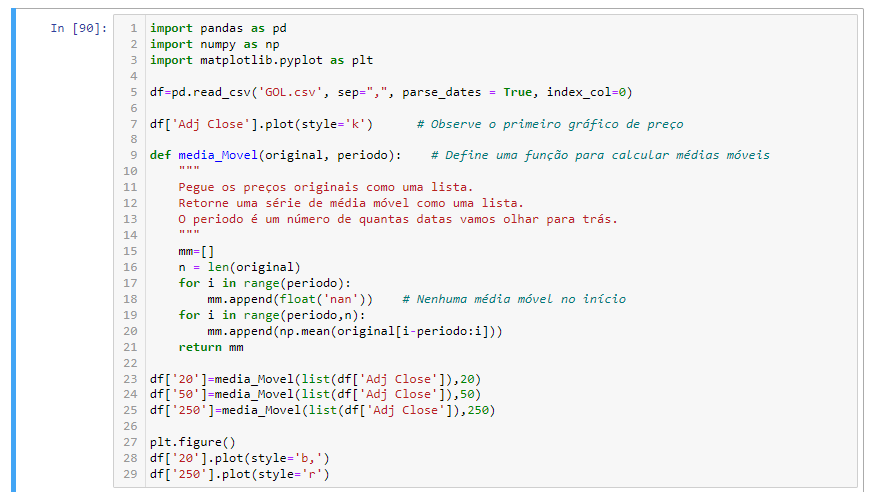
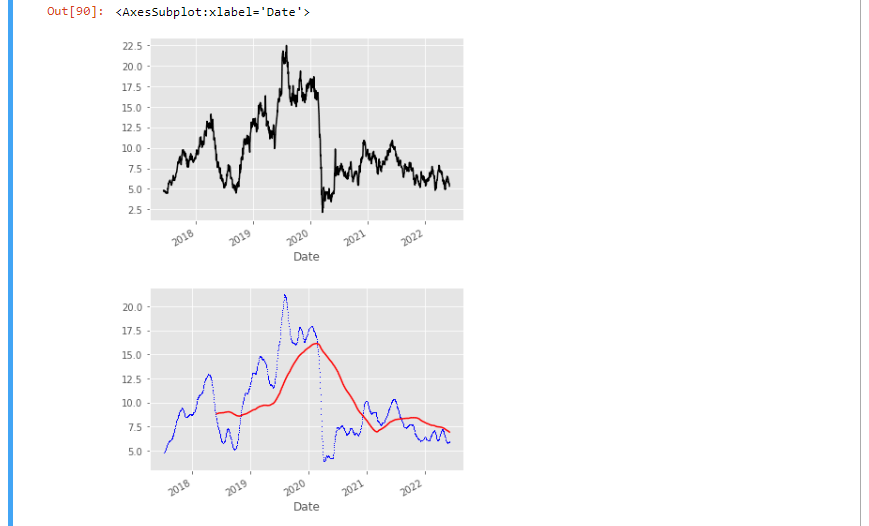
Como você pode ver no gráfico de saída acima, o prazo curto, azul, pontilhado com média móvel de 20 dias cruza o de longo prazo, vermelho, de média móvel de 250 dias abaixo em 2021. Seguindo esse sinal de trading, a GOLL4.SA fez uma corrida espetacular.

Média Móvel de 100 dias

Iremos derivar agora a média móvel de 100 dias. Essa não é a única chave estatística que podemos derivar, mas é aquela uma que iremos tratar agora e você poderá depois brincar com outras funções também.

O que iremos fazer com esse valor é incluí-lo no nosso data frame e compará-lo com o preço da ação daquele dia.

Para isso, primeiro precisaremos criar uma nova coluna. O Pandas faz isso automaticamente quando atribuímos valores a um nome de coluna. Isso significa que não temos que definir explicitamente que estamos criando uma nova coluna.

Ou, mostrando o código de outro jeito:

df['med_Movel_100d']=df['Adj Close'].rolling(window = 100, min_periods=0).mean()

Aqui definimos uma nova coluna com o nome med_Movel_100d. Agora vamos preencher esta coluna com os valores médios de cada 100 entradas. A função rolling empilha uma quantidade específica de entradas. a fim de tornar possível um cálculo estatístico. O parâmetro window é aquele um que define quantas entradas irão ser empilhadas. Mas há também o parâmetro min_periods. Este define quantas entradas precisamos para ter no mínimo a fim de realizar o cálculo. Isso é relevante porque as primeiras entradas do nosso data frame não terão uma centena anteriores a ela. Configurando esse valor para zero começamos os cálculos já com os primeiros números, mesmo se não existir um único valor anterior. Isso tem o efeito que o primeiro valor será apenas o primeiro número, o segundo valor será a média dos dois primeiros números e assim por diante, até obtermos uma centena de valores.

Usando a função mean, estamos obviamente calculando a média aritmética. Entretanto, podemos usar um monte de outras funções como max, min ou median, se quisermos.

Valores NaN

No caso de escolhermos um outro valor diferente de zero para nosso parâmetro min_periods, acabaremos com alguns dos NaN-Values. Eles não são valores numéricos e eles são inúteis. Portanto, vamos querer deletar as entradas que tiverem tais valores.

Fazemos isso usando a função dropna. Se tivermos quaisquer entradas com valores NaN em qualquer coluna, elas agora terão sido deletadas. Podemos dar uma rápida olhada nas colunas do data frame:

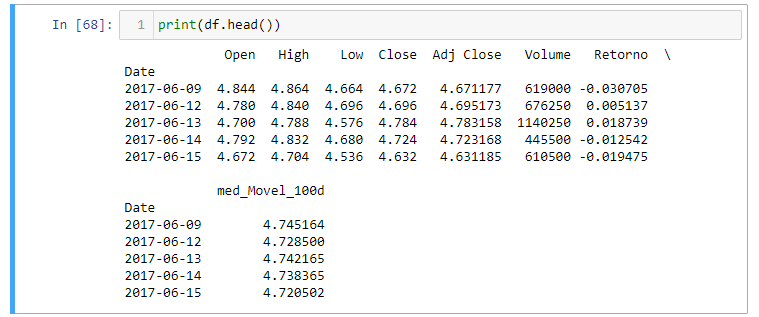
Chaves Estatísticas Adicionais

É claro que existem uma porção de outros valores estatísticos que podemos calcular. Por enquanto, estamos focando somente na maneira de implementação. Entretanto, vamos dar uma rápida olhada a dois outros valores estatísticos importantes:

Variação Porcentual

Um valor que podemos calcular é a variação porcentual daquele dia. Isto significa em quantos porcentos o preço da ação aumentou ou diminuiu naquele dia. O Cálculo é simples. Basta, criarmos uma nova coluna com o nome de Variacao_PCT e os valores são apenas a diferença dos valores de Abertura (Open) e Fechamento (Close), dividido pelos valores de Abertura. Como o valor de abertura é o valor do começo daquele dia, tomamos ele como base. Podemos também multiplicar o resultado por 100 para obter a porcentagem real.

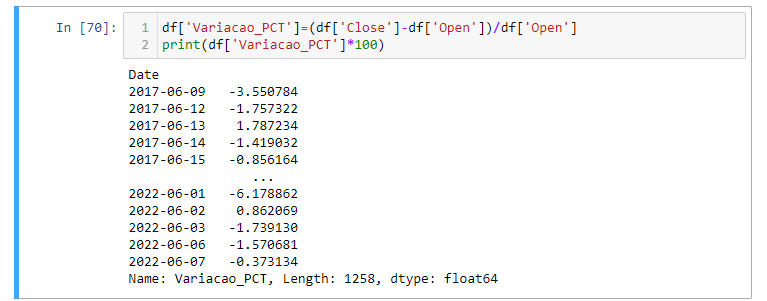
Porcentagem Alta e Baixa

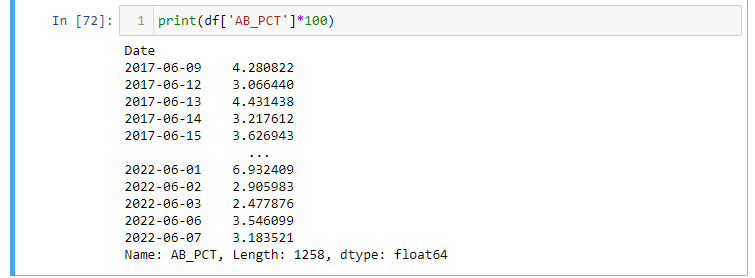
Uma outra estatística interessante é a porcentagem alta e baixa. Aqui apenas calculamos a diferença entre os valores mais alto e mais baixo e os dividimos pelo valor de fechamento. Fazendo isso podemos obter um sentimento de quão volátil é a ação:

Estes valores estatísticos podem ser usados com muitos outros para obter uma porção de informações valiosas sobre ações específicas. Isto melhora a tomada de decisão.

Para uma leitura da teoria sobre suavização exponencial, temos o site do Prof. Bertolo.