O Espírito no Átomo

O QUE É A TEORIA QUÂNTICA?

A palavra "quantum" significa "quantidade" ou "porção discreta". Na escala cotidiana, estamos acostumados à idéia de que as propriedades de um objeto, tais como seu tamanho, peso, cor, temperatura, área superficial e movimento são qualidades que podem variar de um modo suave e contínuo de um objeto a outro. As maçãs, por exemplo, podem apresentar-se com todo tipo de formas, tamanhos e cores sem apreciáveis diferenças entre duas delas.

Entretanto, na escala atômica as coisas são muito diferentes. As propriedades das partículas atômicas, como seu movimento, energia e spin nem sempre apresentam variações suaves, sendo que, pelo contrário, podem diferir em quantidades discretas. Uma das hipóteses da mecânica clássica era que as propriedades da matéria variavam de modo contínuo. Quando os físicos descobriram que esta noção não estava correta na escala atômica, tiveram que desenvolver um sistema de mecânica completamente novo - a mecânica quântica - para levar em conta as características do comportamento atômico da matéria. A teoria quântica é, então, a teoria subjacente da qual deriva a mecânica quântica.

Se se levar em contar o êxito da mecânica clássica na descrição da dinâmica de todas as classes de objetos, desde bolas de bilhar até as estrelas e planetas, não é surpreendente que sua substituição por um novo sistema mecânico fora considerada uma revolução. Entretanto, os físicos provaram em seguida a validade da teoria mediante a explicação de um amplo gama de fenômenos que, de outro modo, seriam incompreensíveis; tanto que hoje em dia a teoria quântica é freqüentemente citada como a teoria mais gloriosa já criada.

ORIGENS

A teoria quântica teve suas origens vacilantes no ano de 1900, com a publicação de um artigo pelo físico alemão Max Planck. Planck dirigiu sua atenção ao que era todavia um problema não resolvido pela física do século XIX, e que consistia na distribuição entre os diversos comprimentos de onda da energia calorífica irradiada por um corpo quente. Sob certas condições ideais, a energia se distribui de um modo característico, que Planck demonstrou que podia ser explicada supondo que a radiação eletromagnética era emitida pelo corpo em pacotes discretos aos quais chamou "quanta". A razão deste comportamento espasmódico era desconhecida, e simplesmente teria que se aceitar ad hoc.

Em 1905 a hipótese quântica foi estimulada por Einstein, quem explicou de modo satisfatório o chamado efeito fotoelétrico, que consiste na extração de elétrons da superfície de um metal mediante energia luminosa. Para explicar o modo particular de como isto se sucede, Einstein viu-se forçado a considerar o raio luminoso como uma chuva de partículas, posteriormente chamadas fótons. Esta descrição da luz parecia estar em confronto direto com a idéia tradicional, segundo a qual a luz (assim como todo tipo de radiação eletromagnética) consiste em ondas contínuas que se propagam de acordo com a célebre teoria eletromagnética de Maxwell, firmemente estabelecida meio século antes. De fato, a natureza ondulatória da luz havia sido demonstrada experimentalmente, em uma época muito remota, por Thomas Young mediante seu famoso aparelho de "da dupla fenda".

A dicotomia onda-partícula, entretanto, não estava restrita à luz. Os físicos da época estavam também interessados na estrutura dos átomos. Em particular, estavam intrigados acerca de como os elétrons podiam girar ao redor do núcleo sem emitir radiação, pois sabia-se pela teoria eletromagnética de Maxwell que quando as partículas carregadas seguem caminhos curvilíneos irradiam energia eletromagnética. Se isto ocorre continuamente, os elétrons atômicos, que estão orbitando em torno do núcleo, perderiam rapidamente energia e cairiam seguindo espirais até este núcleo (veja Fig. 1).

Em 1913 Bohr propôs que os elementos atômicos estão também "quantizados", no sentido de que podem permanecer em certos níveis fixos sem perder energia. Quando os elétrons saltam de um nível a outro, absorve ou emite energia eletromagnética em quantidades discretas. Estes pacotes de energia são, de fato, fótons.

A razão pela qual os elétrons atômicos haviam de comportar-se deste modo descontínuo não foi, entretanto, esclarecida até quando se descobriu a natureza ondulatória da matéria. O trabalho experimental de Clinton Davisson e outros e o trabalho teórico de Louis de Broglie conduziram à idéia de que os elétrons, assim como os fótons, podem comportar-se como ondas e como partículas, dependendo das circunstâncias de cada caso. Segundo a descrição ondulatória, os níveis de energia atômicos propostos por Bohr correspondem a estados de ondas estacionárias ao redor do núcleo. De modo muito parecido ao que se pode fazer numa cavidade ressonante para diferentes notas musicais discretas, assim os elétrons vibram em certos estados definidos de energia. Somente quando, devido à transição de um nível de energia a outro, a estrutura muda, produz-se uma perturbação eletromagnética com emissão ou absorção de radiação.

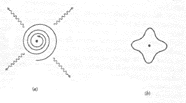
Fig.01 - Colapso do átomo clássico. (a) As teorias de Newton e Maxwell predizem que um elétron atômico que segue uma órbita irradiará continuamente ondas eletromagnéticas, perdendo assim energia e caindo em espiral até o núcleo. (b) A teoria quântica prediz a existência de níveis de energia discretos não radioativos nos quais a onda associada ao elétron precisamente ajusta-se ao redor do núcleo, formando padrões de ondas estacionárias reminescentes das notas num instrumento musical. (A onda deve ajustar-se-á também na direção radial).

Fica claro de imediato que não somente os elétrons, mas todas as partículas subatômicas, estão sujeitas a um comportamento semelhante. Evidentemente, as leis tradicionais da mecânica formulada por Newton, assim como as leis do eletromagnetismo de Maxwell, fracassaram completamente no micromundo dos átomos e das partículas subatômicas. Até a metade da década de 1920, um novo tipo de mecânica - a mecânica quântica - havia sido desenvolvida independentemente por Erwin Schrödinger e Werner Heisenberg para levar em conta esta dualidade onda-partícula.

A nova teoria teve um êxito espetacular. Em seguida ajudou aos cientistas a explicarem a estrutura dos átomos, a radioatividade, a ligação química e os detalhes dos espectros atômicos (incluindo os efeitos dos campos elétricos e magnéticos). Elaborações ulteriores da teoria por Paul Dirac, Enrico Fermi, Max Born e outros conduziram, com o tempo, a explicações satisfatórias da estrutura e reações nucleares, as propriedades elétricas e térmicas dos sólidos, a supercondutividade, a criação e aniquilação de partículas elementares da matéria, a predição da existência de antimatéria, a estabilidade de certas estrelas colapsadas e muito mais. A mecânica quântica tornou possível também um importante projeto em instrumentação prática, que inclui o microscópio eletrônico, o laser e o transistor. Experimentos atômicos tremendamente delicados tem confirmado a existência de sutis efeitos quânticos com um assombroso grau de exatidão. Nenhum experimento conhecido nos últimos cinqüenta anos está em contradição com as predições da mecânica quântica.

Este catálogo de triunfos singulariza a mecânica quântica como uma teoria verdadeiramente notável - uma teoria que descreve corretamente o mundo a um nível de precisão e detalhe sem precedentes na ciência. Hoje em dia, a grande maioria dos físicos profissionais empregam a mecânica quântica, senão quase impensadamente, pelo menos com completa confiança. Contudo, este magnífico edifício teórico está alicerçado sobre um profundo e molesto paradoxo que tem levado alguns físicos a declararem que a teoria não tem sentido finalmente.

O problema, que de fato surgiu nos finais dos anos 1920 e começo dos 1930, tem a ver não com os aspectos técnicos da teoria, mas com a sua interpretação.

ONDAS OU PARTÍCULAS?

A peculiaridade do "quantum" se constata facilmente pelo modo em que um objeto, como um fóton, pode manifestar propriedades ondulatórias e corpusculares. Pode-se fazer com que os fótons produzam figuras de interferência e difração, o que verifica sua natureza ondulatória. Por outro lado, no efeito fotoelétrico os fótons extraem elétrons de um metal colidindo com eles. Neste caso, o modelo corpuscular da luz parece mais apropriado.

A coexistência das propriedades ondulatórias e corpusculares leva rapidamente a algumas conclusões surpreendentes sobre a natureza. Consideremos um exemplo familiar. Suponha que um feixe de luz polarizada incide sobre uma peça de material polarizante (veja a Fig. 2). A teoria eletromagnética ordinária prediz que se o plano de polarização da luz é paralelo ao do material, transmite-se toda a luz. Pelo contrário, se são perpendiculares, não se transmite luz alguma. Para ângulos intermediários se transmite alguma quantidade de luz; por exemplo, a 45º a luz transmitida tem exatamente a metade da intensidade do feixe original. Isto tem sido confirmado experimentalmente.

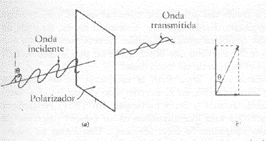
Fig. 02 - A crise de previsibilidade. (a) Classicamente, a luz de onda polarizada atravessará o polarizador com uma intensidade reduzida cos2q emergindo polarizada na direção vertical. Visto como um fluxo de fótons idênticos, este fenômeno pode somente se explicar supondo que alguns fótons passam e outros ficam bloqueados, de modo imprevisível, com probabilidades respectivamente cos2q, sen2q . (b) Note-se que a onda incidente poderia ser considerada como uma superposição de ondas polarizadas verticalmente e horizontalmente.

Pois bem, se a intensidade da luz incidente se reduz de modo que somente um fóton passa de cada vez através do polarizador, encontrar-nos-emos em uma situação paradoxal. Posto que um fóton não pode dividir-se em partes, qualquer um deles deve ou passar ou bem ser bloqueado. Num ângulo de 45º, aproximadamente a metade dos fótons devem ser transmitidos, embora a outra metade seja bloqueada. Mas quais deles passam e quais não passam? Como se supõe que todos os fótons da mesma energia são idênticos e, portanto, indistinguíveis, somos obrigados a concluir que a transmissão de fótons é um processo puramente aleatório. Ainda que qualquer fóton tenha uma probabilidade de 50 % (1/2) de passar, é impossível predizer quais deles em particular o farão. Somente podem-se dar as probabilidades. Ao variar o ângulo, a probabilidade pode mudar de 0 a 1. A conclusão é intrigante e inclusive desconcertante. Antes do descobrimento da física quântica supunha-se que o mundo era completamente previsível, ao menos em princípio. Em particular, se se realizavam experimentos idênticos, esperavam-se resultados idênticos. Mas, no caso dos fótons e o polarizador, podia muito bem ocorrer que dois experimentos idênticos produzissem resultados diferentes, de modo que um fóton passe através do polarizador enquanto que o outro fica bloqueado. Evidentemente, o mundo não é, depois de tudo isso, completamente previsível. Geralmente, até que não se termina uma observação não se pode saber qual será o destino de um fóton dado.

Estas idéias implicam na existência de um elemento de incerteza no micromundo dos fótons, elétrons, átomos e outras partículas. Em 1927, Heisenberg quantificou esta incerteza em seu famoso princípio de indeterminação (ou incerteza). Uma forma de expressar o princípio se refere às tentativas de medir a posição e o momento de um objeto quântico simultaneamente. Especificamente, se, por exemplo, tratamos de localizar muito precisamente um elétron, somos forçados a renunciar a informação sobre seu momento. Reciprocamente, podemos medir o momento do elétron com muita precisão, mas então sua posição fica indeterminada. O simples ato de tentar fixar um elétron específico introduz uma perturbação incontrolável e indeterminada em seu momento e vice-versa. Mais ainda, esta ineludível restrição sobre nosso conhecimento da posição e o momento de um elétron não é meramente conseqüência de uma falta de destreza experimental; é inerente à natureza. Fica claro que o elétron simplesmente não possui posição e momento simultaneamente.

Segue-se então que há no micromundo uma confusão intrínseca que se manifesta sempre que tentamos medir duas quantidades observáveis incompatíveis, tais como a posição e o momento. Entre outras coisas, esta confusão derruba a idéia intuitiva de um elétron (ou fóton, ou qualquer outra partícula) movendo-se segundo uma trajetória espacial bem diferenciada. Para que uma partícula siga uma trajetória bem definida deve possuir em todo instante uma localização (ponto sobre a trajetória) e um momento (vetor tangente à trajetória). Mas uma partícula quântica não pode ter ambas as coisas ao mesmo tempo.

Ordinariamente, supomos que umas leis estritas de causa e efeito dirigem o projétil até seu alvo ou o planeta em sua órbita segundo uma trajetória geométrica exatamente definida no espaço. Não duvidaríamos que, quando o projétil encontra o alvo, seu ponto de colisão representa o ponto final de uma curva contínua que começou no cano da escopeta. Isto não é assim para os elétrons. Podemos diferenciar um ponto de partida e um ponto de chegada, mas nem sempre podemos inferir que havia uma rota definida conectando-os.

Talvez onde esta confusão se mostra mais claramente é no famoso experimento da dupla fenda de Thomas Young (ver Fig.3)

No dito experimento um feixe de fótons (elétrons) provenientes de uma pequena fonte, viaja até uma placa perfurada com duas estreitas aberturas. O feixe cria uma imagem dos buracos sobre uma segunda placa.

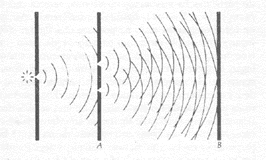
Fig. 03 - Ondas ou partículas? Neste experimento da dupla fenda os elétrons ou fótons da fonte atravessam duas aberturas vizinhas no anteparo A e viajam até incidir no anteparo B, onde se registra seu ritmo de chegada. O padrão de intensidade variável que se observa indica um fenômeno de interferência ondulatória.

A imagem consiste em uma clara mostra de "franjas de interferência" brilhantes e escuras, produzidas ao encontrarem-se as ondas que passam por um buraco com as que passam pelo outro. Nos lugares em que as ondas chegam em fase produz-se um reforço, enquanto onde chegam defasadas produz-se um cancelamento. Assim, pois, a natureza ondulatória dos fótons fica claramente demonstrada.

Mas pode se considerar que o feixe é formado de partículas. Suponha-se que a intensidade do feixe se reduz tanto que somente um fóton ou elétron atravessa cada vez o aparelho. Naturalmente, cada um deles chega a um ponto definido sobre a imagem do anteparo, que pode ser registrada como uma pequena marca. Outras partículas chegam a outros lugares, deixando suas próprias marcas. O efeito parece a princípio aleatório. Mas começa a surgir uma figura do tipo marcado. Cada partícula se dirige a uma lugar particular sobre a imagem no anteparo, não por algum imperativo, mas pela "lei das médias". Quando um grande número de partículas atravessou o sistema, cria-se uma figura organizada. Esta é a figura de interferência. Assim, pois, um dado fóton ou um dado elétron não produz uma figura; somente dá lugar a uma simples marca. Entretanto, cada fóton ou elétron, ainda que em princípio possa ir livremente a qualquer lugar, coopera de modo que a figura de interferência se construa de maneira probabilística. Pois bem, se uma das duas aberturas permanece fechada, o comportamento em média dos elétrons ou fótons muda dramaticamente; de fato, a figura de interferência desaparece. Não pode ser tampouco reconstruída mediante a superposição das duas figuras obtidas registrando as imagens provenientes de cada uma das duas fendas sozinhas. A interferência se manifesta somente quando as duas fendas estão abertas simultaneamente. Portanto, cada fóton ou elétron deve de algum modo dar-se conta individualmente de se ambas fendas, ou só uma delas, estão abertas. Mas como podem fazer se são partículas indivisíveis? Parece evidente que cada partícula possa passar somente através de uma fenda. E, entretanto, a partícula "conhece" de alguma maneira o estado da outra fenda. Como?

Um modo de responder a esta pergunta é recordando que as partículas quânticas não tem trajetórias espaciais bem definidas. As vezes é conveniente imaginar que cada partícula possui de certa maneira uma infinidade de trajetórias diferentes, cada uma das quais contribui ao seu comportamento. Estas trajetórias ou caminhos passam através de ambas fendas e levam informação sobre cada uma delas. Assim é como a partícula se mantém informada do que se sucede em uma região extensa do espaço. A confusão em sua atividade a capacita a "perceber" muitos caminhos diferentes.

Suponha-se que um físico incrédulo colocara detectores diante das duas fendas para saber antecipadamente para qual delas se dirigirá um elétron em particular. Não poderia o físico então fechar num golpe a outra fenda sem que o elétron se "inteire", deixando assim inalterado seu movimento? Se analisarmos a situação, levando em conta o princípio da incerteza de Heisenberg, podemos ver que a natureza acaba vencendo o astuto físico. Se a posição do elétron se mede com a precisão suficiente para poder distinguir de qual fenda se aproxima, perturba-se tanto seu movimento que a figura de interferência aparentemente desaparece! O simples ato de investigar aonde vai o elétron assegura o fracasso da cooperação entre as duas fendas. Somente se decidirmos não marcar o caminho do elétron é quando ela mostrará seu "conhecimento" dos dois caminhos.

John Wheeler assinalou uma intrigante conseqüência da dicotomia que acabou de se mencionar. A decisão de realizar o experimento para determinar a trajetória do elétron ou renunciar a esta informação e, em lugar dela, experimentar com figuras de interferência pode demorar até depois de que qualquer elétron dado tenha atravessado o aparelho! Neste, assim chamado, experimento de "escolha retardada" ("delayed-choce") parece como se o que o experimentador decide agora pudesse influir em algum sentido sobre como as partículas quânticas haviam se comportado no passado, ainda deve-se assinalar que a imprevisibilidade inerente a todos os processos quânticos proíbe que este dispositivo seja usado para enviar sinais para trás no tempo ou para "alterar" de alguma maneira o passado.

Um dispositivo idealizado projetado para realizar um experimento do tipo de escolha-retardada (com fótons, não com elétrons) aparece na Figura 4 e forma a base de um experimento real feito recentemente por Carrol Alley e seus colegas na Universidade de Maryland. Um raio laser incidente sobre um espelho semi-prateado A divide-se em dois feixes análogos aos dois caminhos através das fendas no experimento de Young. Reflexões ulteriores nos espelhos M redirigem os feixes de modo que se cruzam e entram nos detectores 1 e 2, respectivamente. Neste dispositivo uma detecção de um fóton dado, seja por 1 ou por 2, basta para determinar qual dos caminhos alternativos terá o fóton tomado.

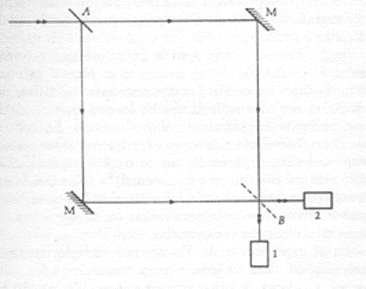
Fig 04 - Diagrama esquemático que mostra o desenho de uma versão prática do experimento de escolha retardada de Wheeler.

Se agora se introduz um segundo espelho semi-prateado no ponto de cruzamento (ver Fig. 4), os dois raios se recombinam, parte em direção a 1 e parte em direção a 2. Isto causará interferências, e as intensidades dos raios que vão a 1 e 2 dependerão das fases relativas dos dois raios no ponto de recombinação. Estas fases podem alternar-se ajustando o comprimento dos caminhos, alterando assim essencialmente o padrão de interferência. Em particular é possível dispor as fases de modo que mediante interferência destrutiva não chegue intensidade a 1, indo toda ela a 2. Deste modo o sistema é análogo ao original experimento de Young, no qual não é possível especificar qual dos dois caminhos o fóton tomou. (Em linguagem coloquial, diríamos que o fóton segue ambos os caminhos)

Agora o ponto crucial é que a decisão de atravessar ou não o segundo espelho B pode demorar-se até que um dado fóton quase tenha chegado ao ponto de cruzamento. Em outras palavras, se o fóton atravessou o sistema por um caminho ou por "ambos" vem determinado somente depois da travessia ter tomado lugar.

QUE SIGNIFICA TUDO ISTO ?

O fato de que os elétrons, fótons e outros objetos quânticos se comportem algumas vezes como partículas e outras vezes como ondas sugere a pergunta de que são "realmente". A postura convencional no que diz respeito a questões desta índole sai de repente dos trabalhos de Bohr, quem acreditou haver descoberto uma interpretação consistente da mecânica quântica. Esta se conhece como a interpretação de Copenhagem, assim chamada pelo instituto de Bohr na Dinamarca, que ele fundou na década de 1920.

Segundo Bohr, não tem sentido perguntar o que é "realmente" um elétron. Ou ao menos, se se coloca a questão, a física não pode dar uma resposta. A física, declarou, não nos diz nada acerca do que é, mas do que podemos comunicarmos sobre o mundo. De concreto, se um físico termina um experimento sobre um sistema quântico, supondo-se que dá uma especificação completa do dispositivo experimental, a física pode então fazer uma predição judiciosa sobre o que o físico poderia observar e conseqüentemente comunicar a seus colegas em uma linguagem compreensível.

No experimento de Young, por exemplo, temos uma escolha clara. Ou deixamos tranqüilos os elétrons e fótons, e observamos sua figura de interferência, ou podemos dar uma olhadela rápida nas trajetórias das partículas e apagar a dita figura. As duas situações não são contraditórias, mas complementares.

De modo similar, existe uma complementaridade posição-momento. Podemos escolher medir a posição de uma partícula em cujo caso seu momento é incerto, ou podemos medir o momento e abandonar o conhecimento de sua posição. Cada uma das qualidades - posição e momento - constitui um aspecto complementar do objeto quântico.

Bohr elevou essas idéias a princípio: o de complementaridade. Na dualidade onda-partícula, por exemplo, as propriedades ondulatórias e corpuscular de um objeto quântico constituem aspectos complementares de seu comportamento. Ele argumentou que não deveríamos encontrar nunca experimentos em que estes dois comportamentos diferentes entram em conflito entre si.

Uma profunda conseqüência das idéias de Bohr é que se altera o tradicional conceito ocidental da relação entre macro e micro, o todo e suas partes. Bohr assegurou que para que tenha sentido falar do que um elétron está fazendo, antes deve se especificar o contexto experimental total; dizer o que se vai medir, como está disposto o aparelho, etc. Assim, pois, a realidade quântica do micromundo está inextrincavelmente ligada com a organização do macromundo. Em outras palavras, a parte não tem sentido exceto em relação com o todo. Este carácter holístico da física quântica tem encontrado uma favorável acolhida entre os seguidores do misticismo oriental, a filosofia encarnada em religiões orientais tais como o Hinduismo, Budismo e Taoísmo. Realmente, nos primeiros momentos da teoria quântica muitos físicos, incluindo Schrödinger, apressaram-se a traçar paralelismos entre o conceito quântico do todo e da parte e o conceito oriental tradicional da unidade harmônica da natureza.

Um conceito central na filosofia de Bohr é a afirmação de que incerteza e confusão são intrínsecas ao mundo quântico e não meramente o resultado de nossa percepção incompleta do mesmo. Isto é um assunto muito sutil. Conhecemos muitos sistemas que são imprevisíveis: as vicissitudes do tempo, a bolsa e a roleta, por exemplo, nos são familiares. Entretanto, tais sistemas não nos forçam a realizar uma reconsideração radical nas leis da física. A razão é que a imprevisibilidade da maioria das coisas cotidiana pode ser esclarecida por não termos informação suficiente para calcular seu comportamento a um nível de detalhe necessário para uma predição exata. No caso da roleta, por exemplo, recorremos a uma descrição estatística. Assim mesmo na termodinâmica clássica se pode descrever adequadamente o comportamento coletivo de miríades de moléculas em média usando mecânica estatística. Entretanto, as flutuações em torno aos valores médios calculados não são nesse caso intrinsecamente indeterminadas porque, em princípio, poderia dar-se uma descrição mecânica completa de cada uma das moléculas em jogo (ignorando neste exemplo os efeitos quânticos!).

Quando se descarta a informação concernente a algumas variáveis dinâmicas, introduz-se um elemento de vacuidade e incerteza em nossa descrição do sistema. Entretanto, sabemos que esta confusão é realmente o resultado da atividade de todas essas variáveis que temos escolhido ignorar. Poderíamos chamá-las "variáveis ocultas". Estão sempre alí, mas nossas observações podem ser demasiadas cruas para fazê-las aparecer. Assim, por exemplo, a medida da pressão de um gás não é suficientemente fina para revelar os movimentos individuais das moléculas.

Por que não podemos atribuir a indeterminação quântica a um nível mais profundo de variáveis ocultas? Uma teoria assim nos capacitaria para descrever a extravagância caótica e aparentemente indeterminada das partículas quânticas como conduzida por um substrato de forças completamente deterministicas. O fato de que parece sermos incapazes de determinar a posição e o momento de um elétron simultaneamente poderia então se atribuir a crua natureza de nosso aparelho, que é também incapaz de sondar o nível mais fino deste substrato.

Einstein estava convencido de que devia ocorrer algo assim; que no final um mundo clássico de causa e efeito familiares reside debaixo da casa de loucos do quantum. Esforçou-se em construir experimentos mentais para verificar a idéia. O mais refinado destes o apresentou em um artigo famoso hoje em dia, escrito em 1935 em colaboração com Boris Padolsky e Nathan Rosen.

O EXPERIMENTO DE EINSTEIN-PODOLSKY-ROSEN (EPR)

O propósito deste experimento ideal era expor as profundas peculiaridades da descrição de um sistema quântico estendido sobre uma região grande do espaço. O experimento nos convida a fazer trapaças ao princípio da incerteza de Heisenberg, olhando de relance a posição e o movimento de uma partícula simultaneamente. A estratégia empregada é usar uma partícula cúmplice para realizar uma medida "com poderes" sobre a partícula de interesse. Suponha-se que uma partícula estacionária fragmenta-se em dois pedaços A e B (veja a Fig. 05). O princípio da incerteza de Heisenberg aparentemente nos proíbe conhecer de maneira simultânea a posição e o momento, seja de A ou de B. Entretanto, devido a lei da ação e reação (conservação do momento), pode-se usar uma medida do momento de B para deduzir o momento de A. De maneira semelhante, por simetria, A terá percorrido uma distância igual à de B desde o ponto de explosão, assim que uma medida da posição de B revela a posição de A.

Um observador em B é livre, a seu capricho, de observar ou bem o momento ou bem a posição de B. Como resultado, conhecerá ou bem o momento ou bem a posição de A, segundo a sua escolha. Em conseqüência, uma observação subsequente de ora o momento , ora a posição de A terá agora um resultado previsível.

Einstein argumentava: "Se, sem perturbar de modo algum um sistema, podemos predizer com certeza..... o valor de uma quantidade física, então existe um elemento de realidade física correspondente a esta quantidade física". Ele, portanto, concluía que na situação descrita a partícula A deve possuir um movimento real ou uma posição real, segundo a escolha do observador em B.

Pois bem, o ponto crucial é o seguinte: Se A e B tiverem separados por um grande trecho, então se é levado a supor que uma medida realizada sobre B pode afetar a A. Ao menos, um pouco, A não pode ser afetada diretamente de modo instantâneo, porque segundo a teoria da relatividade especial nenhum sinal ou influência física pode viajar mais rapidamente que a luz; assim que A não pode "saber" que se tem realizado uma medida sobre B ao menos até o instante em que a luz pudesse chegar a A. Em princípio isto poderia demorar bilhões de anos!!

Bohr refutou o raciocínio de Einstein, reiterando sua filosofia de Copenhagem, de que as propriedades microscópicas de uma partícula quântica devem ser consideradas dentro do contexto macroscópico total. Neste caso uma distante mas correlacionada partícula cúmplice, sujeita a medidas forma uma parte inseparável do sistema quântico. Ainda que nenhum sinal ou influência direta pode viajar entre A e B, isso não significa, segundo Bohr, que podem se ignorar as medidas realizadas sobre B ao discutir as circunstâncias de A. Assim pois, ainda que nenhuma força física real se transmita entre A e B, ambas parecem COOPERAR em seu comportamento numa espécie de conspiração.

Fig. 05 - Dois fragmentos da mesma massa que se emitem de um centro comum (suposto em repouso) tem momentos de igual magnitude e direções opostas e estão sempre eqüidistantes do dito centro. Daí que uma medida da posição ou momento de A revela, respectivamente, a posição ou o momento de B.

Einstein encontrou dificuldade em engolir esta idéia de duas partículas amplamente separadas, que conspiram para dar resultados coordenados de medidas independentes realizadas sobre cada uma delas, ridicularizando-a como "ação à distância fantasma". Ele desejava que sua realidade objetiva se localizará em cada partícula, e foi esta localidade que levaria suas idéias a entrar em conflito com a mecânica quântica. O que se necessitava era uma prova experimental prática que pudesse descriminar entre as idéias de Bohr e Einstein, mostrando a cooperação, ou ação à distância fantasma, em ação. Mas um tal desenvolvimento teve que esperar meio-século.

TEOREMA DE BELL

Em 1965 John Bell estudou o problema dos sistemas quânticos e foi capaz de provar um poderoso teorema matemático que resultou em importância crucial para o desenvolvimento de um teste experimental prático. A teoria é essencialmente independente da natureza das partículas e dos detalhes das forças que atuam sobre elas e se concentra sobre as regras da lógica que governam todos os processos de medidas. Daremos um exemplo simples destas últimas: um censo da população britânica não pode de modo algum descobrir que o número de pessoas negras é maior que o número de homens negros mais o número de mulheres de todas as raças.

Bell investigou as correlações que pudessem existir entre os resultados de medidas realizadas simultaneamente sobre duas partículas separadas . Estas medidas podiam ser de posições, momentos, spin, polarizações e outras variáveis dinâmicas das partículas. Muitos pesquisadores tem adotado a polarização como um meio conveniente de estudar as correlações EPR. Suponha-se que uma partícula com momento angular nulo se desintegre em dois fótons A e B. Devido às leis de conservação, um fóton deve ter a mesma polarização que o outro. Isto pode-se confirmar colocando instrumentos de medida perpendiculares aos caminhos das partículas e medindo a polarização em alguma direção comum, digamos "para cima". Acha-se certamente que quando a partícula A passa através do polarizador, a B também passa. Encontra-se 100% de correlação. E vice-versa, se os polarizadores se colocam perpendiculares entre si, cada vez que passa em A fica bloqueado em B. Neste caso há 100% de anticorrelação. Não há nada misterioso nisto; seria certo também na mecânica clássica ordinária.

O teste crucial surge quando os aparelhos de medida da polarização se orientam obliquamente entre si (Veja Fig. 06). Nesse caso esperaríamos algum resultado intermediário entre correlação completa e anticorrelação completa, dependendo dos ângulos escolhidos. Estes podem ser diversos paralela e perpendicularmente à linha de vôo das partículas e poderiam ser variados aleatóriamente de uma medida à seguinte.

Bell planejou descobrir até que limites teóricos podem estar

correlacionados os resultados de tais medidas. Suponha-se, por exemplo, que Einstein estivesse basicamente certo e que o comportamento quântico é realmente o produto de um substrato de forças clássicas caóticas. Suponha-se também que a propagação dos sinais a velocidades superiores à da luz está proibida de acordo com as regras da teoria da relatividade.

Fig. 06 - O teorema de Bell aplicado a dois fótons em direções opostas, provenientes de uma fonte comum, prediz um limite para o grau de correlação permitido nos resultados das medidas de polarização realizadas separadamente em cada um deles.

Formulada com propriedade, a primeira suposição é o que usualmente se entende por realidade, porque afirma que os objetos quânticos possuem realmente todos os atributos dinâmicos num sentido bem definido em todo momento. A segunda suposição é denominada "localidade" ou às vezes "separabilidade" porque proíbe que os objetos exerçam entre si influências físicas de modo instantâneo quando se encontram separados no espaço.

Aceitando a dupla suposição de "realidade local" e supondo ademais que as regras convencionais da lógica não se vão a pique contra as rochas da incerteza quântica, Bell foi capaz de estabelecer um limite estrito acerca do nível de correlação possível para os resultados de medidas simultâneas sobre as partículas. O "x" da questão é o seguinte. A mecânica quântica de Bohr prediz que sob certas circunstâncias, o grau de cooperação deveria ultrapassar o limite de Bell. Isto é, a visão convencional da mecânica quântica requer um grau de cooperação (ou conspiração) entre sistemas separados que excede o permitido logicamente em qualquer teoria "localmente real". Em conseqüência, o teorema de Bell abre o caminho para um teste direto dos fundamentos da mecânica quântica, assim como para uma discriminação entre a idéia de Einstein de um mundo localmente real e a concepção de Bohr de um mundo algo fantasmagórico, repleto de conspiração subatômica.

O EXPERIMENTO DE ASPECT

Tem-se levado a cabo vários experimentos para verificar a desigualdade de Bell. O de maior êxito entre eles foi comunicado por A. Aspect, J. Dalibard e G. Roger em Physical Review Letters (vol. 39, pg. 1804) em dezembro de 1982.

O experimento consistia em medidas de polarização realizadas sobre pares de fótons que se movem em direções opostas e que tem sido emitidos em transições simples por átomos de cálcio. O dispositivo experimental é mostrado na Fig. 07.

No diagrama, a fonte S usava um feixe de átomos de cálcio excitados por um par de laser (isto é, excitação de dois fótons) a um estado (estado S) que podia somente desexcitar-se mediante uma "cascata" de dois fótons. Ao redor de 6 metros de cada lado da fonte colocou-se um comutador óptico-acústico. O princípio empregado foi explorar o fato de que o índice de refração da água varia ligeiramente com a compressão.

No comutador se estabeleceu um onda ultra-sônica estacionária ao redor de 25 MHz usando transdutores dirigidos em sentidos opostos. Fazendo com que os fótons incidissem sobre o comutador com um ângulo próximo do ângulo crítico de reflexão total, era possível trocar as condições de transmissão ou de reflexão em cada semiciclo da onda sonora, quer dizer, a 50 MHz.

Os fótons, ao imergirem segundo a linha da trajetória incidente (através da transmissão) ou desviados (por reflexão) se encontravam com polarizadores, os quais os transmitiriam ou bloqueariam com certas probabilidades definidas. Estes polarizadores estavam orientados segundo ângulos diferentes relativos à polarização dos fótons. O destino dos fótons se monitorava colocando detectores fotomultiplicadores por detrás dos ditos polarizadores. A montagem era idêntica em ambos lados da fonte.

O experimento se realizou monitorando eletronicamente o destino de cada par de fótons e determinando o nível de correlação. A única e essencial característica deste experimento é a capacidade de trocar aleatóriamente, embora os fótons estejam na metade de seus vôos, o caminho subsequente dos fótons, isto é, a qual polarizador serão dirigidos. Isto é equivalente a reordenar os polarizadores de cada lado da fonte tão rapidamente que nenhum sinal pudesse ter tempo suficiente para passar de um ao outro, inclusive à velocidade da luz.

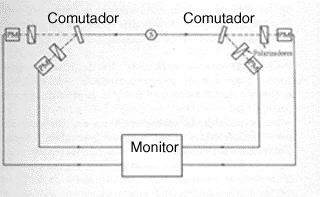
Fig. 07 - Montagem experimental de Aspect. Pares de fótons viajam vários metros da fonte S até os comutadores óptico-acústico. A rota do fóton depois do comutador determina qual dos polarizadores diferentemente orientados encontrará o mesmo. Os fótons são detectados usando fotomultiplicadores (PM) e as coincidências entre os diferentes canais são registrados eletronicamente. A fotografia mostra o dispositivo experimental real. (Cortesia de A. Aspect)

Cada comutação dura ao redor de 10 ns (nanosegundos), o que se compara com a vida média da emissão dos fótons (5 ns) e o tempo de viagem destes (40 ns).

Na prática, a comutação não era estritamente aleatória. As ondas estacionárias geravam-se independentemente a freqüências diferentes. A diferença entre este tipo de comutação e outro verdadeiramente aleatório é irrelevante, exceto no caso das teorias de variáveis ocultas com "conspiração" extremamente irmanada.

Os autores informam que esta sessão típica durava 12.000 s, divididos igualmente entre a disposição descrita mais acima, outra em que se retiraram os polarizadores e uma terceira em que se tirava um polarizador de cada lado. Isto permitiu corrigir os erros sistemáticos nos resultados.

A NATUREZA DA REALIDADE

O resultado do teste mencionado acima é muito mais que um simples esclarecimento de um assunto técnico entre duas teorias rivais do micromundo. O debate concerne a nossa concepção do universo e da natureza da realidade.

Antes dos dias da mecânica quântica, a maioria dos cientistas ocidentais supunham que o mundo ao nosso redor goza de uma existência independente. Isto é, consiste em objetos como mesas, cadeiras, estrelas, átomos, que estão simplesmente "por aí afora ", ainda que os observemos ou não. Segundo esta filosofia, o universo é uma coleção de tais objetos existentes independentemente, que juntos formam a totalidade das coisas. Naturalmente, tem-se que admitir que uma observação que chegamos de um objeto leva consigo alguma interação com ele, o que implica que sofrerá inevitavelmente alguma perturbação. Entretanto, esta é considerada como uma perturbação incidental sobre algo que já possui uma existência concreta e bem definida. Certamente, em princípio, a perturbação necessária para medir algo poderia se fazer arbitrariamente pequena e, em qualquer caso, poderia ser calculada com todo detalhe, de modo que depois da medida poderíamos deduzir exatamente o que havia ocorrido ao objeto observado. Se este fora o caso de verdade, não vacilaríamos em dizer que o objeto tinha realmente um conjunto completo de atributos dinâmicos como posição, momento, spin e energia antes e depois da observação do mesmo. Os átomos e os elétrons seriam então simplesmente "coisas pequenas", diferindo das "coisas grandes", tais como bolas de bilhar, somente em matéria de escala. Salvo isso, não há diferenças qualitativas em sua categoria dentro do real.

Esta descrição do mundo é atraente porque é a que se dá melhor com o nosso sentido comum de entender a natureza. Einstein a chamava de "realidade objetiva" porque o status dentro da realidade dos objetos externos não depende das observações conscientes de um indivíduo. (Em contraste com os objetos em nossos sonhos, que são partes da realidade subjetiva). Mas é precisamente esta visão de sentido comum da realidade que Bohr desafiou com a filosofia que acompanha à interpretação de Copenhagem.

A posição de Bohr, como já se tem dito, é que não tem sentido descrever um conjunto completo de atributos de algum objeto quântico antes de ter realizado sobre ele um ato de medida. Assim, por exemplo, em um experimento de polarização de fótons não podemos simplesmente dizer qual polarização tem um fóton antes que tenhamos feito uma medida. Mas depois da medida podemos certamente atribuir um estado de polarização definida ao fóton. Similarmente, se nos enfrentarmos com a escolha de medir a posição ou o momento de uma partícula, não podemos dizer que a partícula possui valores específicos destas quantidades antes da medida. Se decidirmos medir a posição, acabamos com uma partícula em um lugar. Se, em lugar dela, escolhermos medir o momento, obteremos uma partícula com um movimento. No primeiro caso, depois de acabar a medida, a partícula simplesmente não tem um momento; no último caso não tem uma localização.

Estas idéias podem ser ilustradas com a ajuda de um exemplo simples (veja a Fig 08). Considere uma caixa em que se introduz um único elétron. Na ausência de observações, o elétron tem a mesma probabilidade de estar em qualquer parte da caixa. A onda mecânico quântica que corresponde ao elétron, portanto, estende-se uniformemente por toda a caixa. Suponha-se agora que um anteparo impenetrável é introduzido na metade da caixa, dividindo-a em duas câmaras. Obviamente, o elétron pode somente estar ou na uma câmara ou na outra. Entretanto, até olharmos e vermos em qual, a onda seguirá estando em ambas as câmaras. Após a observação, o elétron se revelará em uma câmara particular. Nesse mesmo instante (segundo as regras da mecânica quântica) a onda desaparece

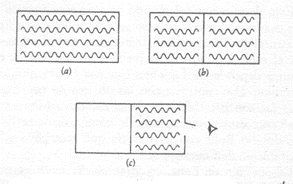
Fig. 08 - Colapso da onda quântica. (a) Quando uma partícula quântica única é confinada numa caixa sua onda associada se esparrama uniformemente em todo seu interior. (b) Insere-se um anteparo que divide a caixa em dois compartimentos isolados. (c) Uma observação revela que a partícula está no compartimento da direita. Bruscamente, a onda no outro compartimento, que representa a probabilidade de que a partícula esteja ali, desaparece.

bruscamente da câmara vazia, inclusive se a câmara permaneceu fechada durante o processo!!! É como se, antes da observação, houvessem dois nebulosos elétrons "fantasmas" que habitam cada uma das câmaras e esperam uma observação que converta um deles em um elétron "real" e que, simultaneamente, causa o completo desaparecimento do outro.

Este exemplo também ilustra claramente a não-localidade da mecânica quântica. Suponha-se que se separam as duas câmaras, A e B, e se levam a uma certa distância uma da outra (digamos um ano-luz); então A é inspecionada por um observador que encontra a partícula. Instantaneamente, a onda quântica em B desaparece, inclusive ainda quando está a um ano-luz de distância. (Deve repetir-se, entretanto, que isto não pode ser usado para enviar sinais mais rápidos do que a luz, devido à natureza imprevisível de cada observação).

Em geral, um sistema quântico se encontrará em um estado que consiste numa coleção (talvez um número infinito) de estados quânticos superpostos. Um exemplo simples de uma superposição assim foi dado mais acima e consistia em duas amostras ondulatórias desconexas, uma em cada câmara. Um exemplo mais típico é o do experimento de Young da dupla fenda, onde as ondas procedentes de ambas fendas de fato se juntam e interferem entre si.

Temos já encontrado esta classe de superposição anteriormente, ao discutir a luz polarizada que atravessa um polarizador orientado obliquamente. Se a onda luminosa incidente forma 45º com o polarizador, podemos considerá-la como formada por duas ondas de igual intensidade combinadas coerentemente com polarizadores perpendiculares entre si, como se tem mostrado na Fig 02. A onda paralela ao polarizador será transmitida, a outra será bloqueada. Poderíamos considerar a um estado quântico que contém um fóton polarizado a 45 com respeito ao polarizador, como uma superposição de dois "fantasmas" ou fótons "potenciais", um com polarização paralela, o que capacita a passar através do polarizador, e outro com polarização perpendicular, o que o impede de passar. Quando finalmente se faz a medida, um desses dois "fantasmas" é promovido a fóton "real" e o outro desaparece. Suponha que a medida mostra que o fóton passa através do polarizador. O fóton fantasma que é paralelo ao polarizador antes da medida se converte então no fóton real. Mas não podemos dizer que este fóton existia realmente antes da medida. Tudo o que se pode dizer é que o sistema estava em uma superposição de dois estados quânticos, nenhum dos quais possuía um estado privilegiado.

O físico John Wheeler gosta de contar uma deliciosa parábola que ilustra muito bem o estado peculiar de uma partícula quântica antes da medida. A história tem a ver com uma versão do jogo das 20 perguntas.

Então chegou a minha vez, o quarto a sair da sala de modo que os outros quinze convidados de Lothar Nordheim pudessem confabular em segredo para se chegar a um acordo sobre a palavra difícil. Estive fora por um tempo incrivelmente grande. Quando finalmente fui readmitido, encontrei que todos estavam sorrindo, sinal de brincadeira ou conspiração. Entretanto, pensei em tentar descobrir a palavra. "É animal?" "Não". "É mineral?" "Sim". "É verde?" "Não". "É branco?" "Sim". As respostas chegavam rapidamente. Então a partir daí as perguntas precisavam de mais tempo para ser respondidas. Era estranho. Tudo o que eu queria dos meus amigos era simplesmente um sim ou um não. Entretanto, o perguntado pensava e pensava, sim ou não, não ou sim, antes de responder. Finalmente tive fortes suspeitas de que a palavra poderia ser "nuvem". Sabia que tinha somente uma oportunidade para dizer a palavra. Aventurei-me: "É nuvem?" "Sim", disseram, e todos caíram em gargalhadas. Explicaram-me que não havia nenhuma palavra no começo. Haviam concordado em não chegar a um acordo sobre nenhuma palavra. Cada um dos perguntados poderia responder como quisesse, com o único requisito de que devia ter em mente uma palavra compatível com a sua própria resposta e com as dadas anteriormente, pois de outro modo perderiam se eu cumprisse o meu intento. A versão surpresa do jogo das vinte perguntas era, portanto, tão difícil para meus colegas como era para mim. Qual o simbolismo da história? O mundo, uma vez criado, existe "mesmo", independente de qualquer ato de observação. Considerávamos o elétron no átomo como possuidor de posição e momento definidos. Quando eu entrava, pensava que na sala havia uma palavra definida. Realmente, a palavra foi desenvolvida passo a passo mediante as perguntas que eu fazia, como a informação acerca do elétron se faz existente pelo experimento que o observador escolheu realizar; isto é, pelo tipo de equipamento de registro que este coloca. Se eu houvesse feito perguntas diferentes ou as mesmas perguntas em ordem diferente, haveria acabado com uma palavra diferente, assim como o experimentador teria concluído uma história diferente dos fatos do elétron. Entretanto, o poder que eu tinha de trazer à existência em particular a palavra "nuvem" era somente parcial. Uma importante parte da seleção reside nos "sim" e "não" dos colegas da sala. De modo semelhante, o experimentador tem uma influência substancial acerca do que sucederá ao elétron mediante a escolha dos experimentos que realizará sobre este, "as perguntas que fará à natureza"; mas ele sabe que existe uma certa imprevisão acerca do que um qualquer dos seus experimentos averiguará, acerca de qual "resposta dará a natureza", acerca do que sucederá quando "Deus joga os dados". Esta comparação entre o mundo das observações e a versão surpresa do jogo das vinte perguntas é muito incompleta, mas contém o ponto decisivo. No jogo, nenhuma palavra é uma palavra até que essa palavra é promovida à realidade pela escolha das perguntas formuladas e respostas dadas. No mundo real da física quântica, nenhum fenômeno elementar é um fenômeno até que seja um fenômeno registrado.

A visão da realidade da escola de Copenhagem é, portanto, decididamente rara. Significa que um átomo ou um elétron ou qualquer outra partícula não pode ser dita existir por si mesma na acepção completa, de sentido comum, da palavra.

Isto, naturalmente, coloca com urgência a pergunta: O que é um elétron? Se não é algo de "externo", existente por direito próprio, por quê podemos falar tão confiadamente acerca dos elétrons?

A filosofia de Bohr parece relegar os elétrons e outras entidades quânticas a um estado bastante abstrato. Por outro lado, se vamos simplesmente adiante e aplicamos as regras da mecânica quântica como se o elétron fosse real, então, parece que obtemos os resultados corretos; podemos dar respostas a todas as perguntas físicas bem formuladas, como quanta energia tem um elétron atômico, e obter acordo com os experimentos.

Um cálculo típico que envolve elétrons consiste na computação da vida média do estado excitado de um átomo. Se sabemos que o átomo está excitado no instante t1 , então a mecânica quântica capacita-nos a calcular a probabilidade de que em algum instante posterior t₂ já não o está. Assim, pois, a mecânica quântica nos proporciona um ALGORITMO para relacionar duas observações, uma em t₁ e a outra em t₂. O chamado "átomo" entra aqui como um modelo que capacita o algoritmo para predizer um resultado específico. Nunca observamos diretamente o átomo durante o processo de desexcitação. Tudo o que sabemos acerca dele está contido nas observações de sua energia em t₁ e t₂. Claramente, não necessitamos supor acerca do átomo nada mais que o necessário para obter resultados satisfatórios para nossas predições de observações reais.

A filosofia segundo a qual a realidade do mundo está enraizada nas observações é semelhante ao conhecido como positivismo lógico. Parece, talvez, alheio a nós porque, na maioria dos casos, o mundo segue comportando-se COMO SE tivesse uma existência independente. Somente quando testamos fenômenos quânticos esta impressão parece como insustentável. Inclusive então, em seu trabalho pratico, muitos físicos continuam pensando sobre o micromundo da maneira do senso comum.

A razão para isto é que muitos dos conceitos matemáticos puramente abstratos empregados se tornam tão familiares que assumem um ar espúrio de realidade por próprio direito. Isto também acontece na física clássica. Considere o conceito de energia, por exemplo. A energia é uma quantidade puramente abstrata, que se introduz na física como um modelo útil com o qual podemos abreviar os cálculos complexos. A energia não se pode ver nem tocar, entretanto, a palavra é agora tão cotidiana que a gente considera a energia como uma entidade tangível com uma existência própria. Na realidade, a energia é meramente uma parte de um conjunto de relações matemáticas que conectam de um modo simples as observações de processos mecânicos. O que sugere a filosofia de Bohr é que palavras como o elétron, fóton ou átomo tem de se considerar do mesmo modo - como modelos úteis que consolidam na nossa imaginação o que realmente é só um conjunto de relações matemáticas que conectam várias observações.

O PARADOXO DA MEDIDA

A chamada interpretação de Copenhagem, apesar de seus efeitos estranhos, é realmente o ponto de vista "oficial" entre os físicos profissionais. Na aplicação prática da mecânica quântica o físico raramente se choca com problemas epistemológicos. Tanto quanto as regras quânticas se aplicam sistematicamente, a teoria proporciona tudo o que dela se pode esperar; isto é, prediz corretamente os resultados de medidas reais - o qual é, além do mais, a ocupação dos físicos-. Entretanto, alguns físicos não se tem contentado com isso, porque no mais profundo da interpretação de Copenhagem parece existir um paradoxo devastador.

De importância capital para o ponto de vista de Bohr é que podemos geralmente falar com sentido dos atributos físicos de um sistema somente depois de que se tem feito uma medida (uma observação) específica. Claramente, isto proporciona um estado físico crucial e especial à medida. Como temos visto, a especificação do contexto da medida requer afirmações particulares acerca do tipo e da localização do aparelho. Isto fica implícito que todos podemos estar de acordo sobre o significado que se dá a frases como "um contador Geiger colocado a dois metros da fonte". O problema aparece quando perguntamos de onde se coloca a linha divisória entre um sistema quântico e uma peça de um aparelho microscópico. Além do mais, os contadores Geiger são por sua vez feitos de átomos e sujeitos ao comportamento quântico.

Segundo as regras da mecânica quântica, um sistema quântico pode evoluir temporariamente de duas maneiras completamente distintas. Se o sistema pode ser considerado isolado, seu desenvolvimento temporal vem descrito pelo que os matemáticos chamam uma operação unitária. Em termos mais físicos, um desenvolvimento unitário corresponde a algo como o seguinte: Suponha-se que o estado do sistema consiste em várias figuras ondulatórias superpostas (ver Fig. 19). As diferentes ondas componentes interferirão continuamente entre si e produzirão uma figura complexa e mutante, análoga às ondulações da superfície de um tanque. De fato, a descrição desta evolução quântica é muito parecida à de qualquer outro sistema do tipo ondulatório.

Em contraposição a isto, suponha-se agora que se faz um certo tipo de medida. O efeito é dramático. De repente desaparecem todas as ondas que contribuíam à figura salvo uma, deixando somente a figura dada por esta única onda que corresponde à "resposta". Cessam os efeitos de interferência e a figura ondulatória subsequente fica totalmente transformada (um exemplo disto se deu na pag. 21). Tal evolução tipo-medida da onda é irreversível. Não podemos desfazê-la e restaurar a complexa figura ondulatória original. Matemáticamente, esta transição é "não-unitária".

Como podemos compreender estes dois modos de comportamento diferentes de um sistema quântico? Obviamente, a troca brusca que ocorre quando tem lugar uma medida tem de estar relacionada com o fato que o sistema quântico se acopla a um aparelho de medida com o qual interage. Já não está isolado. O matemático J. von Neumann procurou provar para um sistema modelo que um acoplamento assim terá certamente os efeitos mencionados. Entretanto, encontramo-nos mais uma vez com o paradoxo fundamental da medida. O aparelho de medida é feito de átomos e, portanto, sujeito às regras do comportamento quântico. Na prática não notamos nenhum efeito quântico em instrumentos macroscópicos porque os ditos efeitos são pequenos. Não obstante, se a mecânica quântica é uma teoria consistente, os efeitos quânticos devem estar presentes, não importa quão grande possa ser o aparelho. Poderíamos então escolher em considerar o sistema acoplado, objeto medido mais aparelho de medida, como um sistema quântico único e grande. Mas, supondo que o sistema combinado possa considerar-se isolado de outros sistemas ulteriores, as mesmas regras da mecânica quântica se aplicam agora aos maiores, incluindo a regra de desenvolvimento unitário.

Por que isto é um problema? Suponha-se que o sistema quântico original se achava em uma superposição de dois estados. Recorde-se, por exemplo, o caso da luz polarizada a 45º com respeito ao polarizador, na qual o estado incidente é uma superposição de dois estados possíveis do fóton, um paralelo e outro perpendicular ao polarizador. O propósito da medida é ver se o fóton atravessa o polarizador ou fica bloqueado por este. O aparelho de medida terá dois estados macroscópicos, cada um deles correlacionados com um dos dois estados de polarização do fóton. O problema é que, de acordo com as leis da mecânica quântica aplicadas ao sistema combinado, o aparelho passa agora a estar em uma superposição de estados! Certamente, se o dispositivo se designa adequadamente, qualquer efeito de interferência causado pelo solapamento (interferência) destes dois estados será minúsculo. Mas, em princípio, os efeitos estão aí, e somos forçados a concluir que o aparelho está agora na classe de estado limbo indeterminado que temos chegado a aceitar para elétrons, fótons, etc.

Von Neumann concluiu que deve arbitrar-se que o aparelho de medida tenha levado a cabo realmente um ato de medida irreversível somente quando ele também está sujeito a uma medida e, em conseqüência, requerido a "tomar uma decisão" (denominado teoricamente o colapso da função de ondas em auto estado particular). Mas agora caímos numa regressão infinita, pois este segundo dispositivo de medida requer assim mesmo outro dispositivo que o "colapse" em um estado de velocidade concreta e assim sucessivamente. É como se o acoplamento de um aparelho a um sistema quântico capacitara à superposição tipo fantasma de estados quânticos para invadir-se o laboratório!! Esta capacidade que temos de por objetos macroscópicos em uma superposição quântica demonstra de modo dramático a peculiaridade da teoria quântica.

O PARADOXO DO GATO DE SCHRÖDINGER, E PIOR

Em 1935 Erwin Schrödinger, um dos fundadores da mecânica quântica, havia já percebido como os problemas filosóficos de uma superposição quântica poderiam aparecer a nível macroscópico. Ilustrou este ponto, dando-lhe um toque de espetacularidade, com um experimento ideal, agora famoso, que tem a ver com um gato (Fig.9)

___________________________________________________________________________________

Um gato está fechado em uma câmara de aço, junto ao diabólico dispositivo seguinte ( que deve assegurar-se contra uma interferência direta por parte do gato); num contador Geiger há um pedacinho de uma substância radioativa, tão pequeno, que talvez no transcurso de uma hora se desintegre um átomo, mas também poderia ocorrer com igual probabilidade que nenhum átomo se desintegrasse; se ocorre o primeiro, produz-se uma descarga no tubo e mediante um relê libera-se um martelo que rompe um frasquinho de ácido cianídrico. Se se deseja que o sistema completo funcione durante uma hora, diríamos que o gato viverá se nesse tempo não tenha desintegrado nenhum átomo. A primeira desintegração atômica o envenenará.

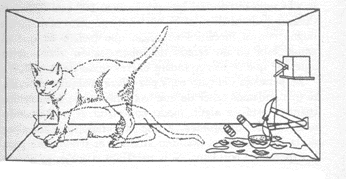
Fig. 09 - O paradoxo do gato de Schrödinger. O dispositivo do veneno é um meio de ampliar a superposição quântica de estados numa escala macroscópica, onde parece estar implicada uma coexistência paradóxica de gatos vivos e mortos (De S.B. De Witt (1970), “Quantum mechanics and reality”, Physics Today, 23,9).

Nas nossa mentes está absolutamente claro que o gato deve estar vivo OU morto. Por outro lado, segundo as regras da mecânica quântica, o sistema total dentro da caixa se encontra numa superposição de dois estados um com o gato vivo e o outro com o gato morto. Mas qual sentido podemos dar a um gato vivo-morto?

É de se presumir que o gato mesmo sabe se está morto ou vivo, e, entretanto, aceita-se a linha de raciocínio de von Neumann, somos obrigado a concluir que a infeliz criatura permanece num estado de animação suspensa até que alguém olha para o interior da caixa para verificá-lo, em cujo momento é projetado à vitalidade plena ou então instantaneamente liquidado.

O paradoxo resulta ainda mais ousado se o gato é substituído por uma pessoa, pois então o amigo que ficou encarcerado dentro da caixa estará consciente todo o tempo de sua saúde ou do contrário. Se o experimentador abre a caixa e descobre que o sujeito está todavia vivo, pode então perguntar a seu amigo como se sentia antes desta aparentemente crucial observação. Obviamente, o amigo responderá que permaneceu 100% vivo durante todo o tempo. E, entretanto, isto se acha em contradição com a mecânica quântica, que insiste em que o amigo está em um estado de superposição vivo-morto antes de se inspecionar o conteúdo da caixa.

O paradoxo do gato derruba qualquer esperança que possamos ter de que o fantasma da mecânica quântica está de algum modo confinado ao micromundo sombrio dos átomos, e que a natureza paradoxal da realidade no domínio atômico é irrelevante para a experiência cotidiana. Se a mecânica quântica é aceita como uma descrição correta de todo tipo de matéria, a dita esperança está claramente fora de lugar. Seguindo a lógica da teoria quântica até sua conclusão final, a maior parte do universo físico parece diluir-se em uma fantasia de sombras.

Einstein, entre outros, não pode jamais aceitar esse extremo lógico. De fato, uma vez perguntou: A lua existe ou não quando alguém está olhando? A idéia de fazer ao observador o elemento pivô na realidade física parece contrário ao espírito inteiro da ciência como um empreendimento impessoal e objetivo. A não ser que exista um mundo concreto "externo" para que experimentemos sobre ele e conjeturemos acerca do mesmo, não degenera a ciência num jogo de trapaças simples de imagens?

Assim, pois, qual é a solução do paradoxo da medida? Aqui é realmente onde entram nossos interlocutores porque, como veremos, tem muitas diferentes opiniões. Examinemos primeiro algumas posturas gerais.

O PONTO DE VISTA PRAGMÁTICO

A maioria dos físicos não levam a lógica da teoria quântica até seu autêntico final. Supõe tacitamente que em alguma parte, a certo nível entre os átomos e os contadores Geiger, a física quântica de algum modo se "converte" na física clássica, no que nunca se duvida acerca da realidade independente de mesas, cadeiras e luas. Bohr disse que esta metamorfose requeria "um ato de amplificação irreversível" da perturbação quântica, que conduza a um resultado detectável macroscopicamente. Mas deixou sem esclarecer o que supõe exatamente este ato.

A MENTE SOBRE A MATÉRIA

O papel chave que desempenham as observações na física quântica leva indubitavelmente a questões sobre a natureza da mente e a consciência e suas relações com a matéria. O fato de que, uma vez tendo levado uma observação sobre um sistema quântico, seu estado (função de ondas) mudará em geral bruscamente, parece familiar à idéia da "mente sobre a matéria". É como se o estado mental alterado do experimentador, ao se conscientizar do resultado da medida, de algum modo se reintroduzirá no aparelho do laboratório e, portanto, no sistema quântico, alterando também seu estado. Brevemente, o estado físico atua alterando o estado mental e o estado mental retroatua sobre o estado físico.

Numa seção anterior mencionou-se como von Neumann imaginava uma cadeia de instrumentos de medidas aparentemente sem fim, no qual cada um deles "observa" o precedente, mas nenhum leva jamais a cabo o "colapso" da função de ondas. A cadeia pode então acabar quando se envolve um observador consciente. Somente com a entrada do resultado da medida na consciência de alguém, a pirâmide completa dos estados quânticos "limbo" colapsará com uma realidade concreta.

Eugene Wigner é um físico que tem propugnado firmemente esta versão dos fatos. Segundo Wigner, a mente desempenha a parte fundamental na realização da brusca troca irreversível no estado quântico que caracteriza uma medida. Não é suficiente equipar o laboratório com complicados instrumentos automáticos de registros, câmaras de vídeo e outros parecidos. Salvo se alguém realmente olha para ver onde marca a agulha no contador (ou realmente olhe o registro vídeo), o estado quântico permanecerá no limbo.

Na última seção vimos como Schrödinger empregou um gato em seu experimento mental. Um gato é um sistema macroscópico suficientemente complexo para que dois estados alternativos (vivo ou morto) sejam dramaticamente distintos. Não obstante, um gato é o bastante complexo para se contar como um observador e alterar irreversivelmente o estado quântico ( isto é, "o colapso da função de ondas"? E se o gato pode fá-lo, o que se passa com uma mosca? Ou com uma pulga? Ou com uma ameba? Onde entra pela primeira vez a consciência na elaboração da hierarquia da vida terrestre?

As considerações precedentes estão intimamente conectadas com a debatida questão do problema corpo-mente na filosofia. Durante muito tempo, muita gente aderiu ao que o filósofo Gilbert Ryle chamava "ponto de vista oficial" sobre a relação entre a mente e o corpo (ou cérebro), que remonta pelo menos até Descartes. Segundo este ponto de vista, a mente (ou alma) é um tipo de substância, um tipo especial de substância efêmera e intangível, diferente do tipo muito tangível de material do que são feitos nossos corpos, mas acoplada a este material. A mente, então, é uma COISA que pode ter estados - estados mentais - que podem alterar-se ( ao receber dados sensoriais) como resultado de seu acoplamento ao cérebro. Mas isso não é tudo. O eslabón que acopla cerebro e mente funciona em dois sentidos, capacitando-nos a gravar nossa vontade sobre nossos cérebro s e por ele sobre nossos corpos.

Hoje em dia, entretanto, estas idéias dualísticas tem caído em desgraça entre muitos cientistas que preferem considerar o cérebro como uma máquina elétrica enormemente complexa, mas sem nenhum mistério a parte, sujeita às leis da física como qualquer outra máquina. Os estados internos do cérebro devem estar determinados, portanto, por seus estados passados mais do que pelos efeitos de quaisquer dados pessoais que entrem nele. Do mesmo modo , os sinais emitidos pelo cérebro, que controlam o que chamamos "comportamento", estão completamente determinados pelo estado interno do cérebro no correspondente momento.

A dificuldade com esta descrição materialista do cérebro é que parece reduzir as pessoas a simples autômatos, não deixando lugar algum para uma mente independente ou uma vontade livre. Se todo impulso nervoso é regulado pelas leis da física, como pode a mente introduzir-se em sua operação? Mas se a mente não se introduz, como é que aparentemente controlamos nossos corpos segundo nossa vontade pessoal?

Com o descobrimento da mecânica quântica, um certo número de pessoas, notadamente Artur Eddington, acreditaram que haviam superado este impasse. Posto que os sistemas quânticos são inerentemente indeterminísticos, a descrição mecânica de todos os sistemas físicos, inclusive o cérebro, torna-se falsa. O princípio da incerteza de Heisenberg permite usualmente uma gama de resultados possíveis para qualquer estado físico dado e é fácil conjecturar que a consciência, ou a mente, poderia ter voto ao decidir qual das alternativas disponíveis se leva realmente a cabo.

Imagine-se então um elétron em alguma célula cerebral a ponto de excitar-se. A mecânica quântica permite que o elétron vague por um conjunto de trajetórias. Talvez, para que a célula se excite, basta que a mente carregue um pouco o dado quântico e assim empurre o elétron, favorecendo uma certa direção e iniciando desse modo uma cascata de atividades elétricas que culmine, digamos no levantamento de um braço.

Independentemente de seu atrativo, a idéia de que a mente acha a sua expressão no mundo por deferência do princípio quântico de incerteza não é tomada realmente muito a sério, em grande parte porque a atividade elétrica do cérebro parece ser mais vigorosa que tudo isso. Depois de tudo, se as células cerebrais operam a nível quântico, a rede inteira é vulnerável às singulares flutuações quânticas aleatórias de qualquer elétron dentre a miríade deles.

O conceito de que a mente é uma entidade capaz de interagir com a matéria tem sido criticado severamente como um erro categórico por Ryle, que ridiculariza o "ponto de vista oficial" da mente, qualificando-a como "o espirito na máquina". Ryle pontualiza que quando falamos de cérebro empregamos conceitos apropriados para um certo nível de descrição. Por outro lado, a discussão sobre a mente faz referência a um nível de descrição completamente diferente e mais abstrato. É algo assim como a diferença entre Governo e a Constituição britânicos, onde o primeiro é um grupo concreto de indivíduos e a última um conjunto abstrato de idéias. Ryle argumenta que tem tão pouco sentido falar de comunicação entre Governo e Constituição como falar de comunicação entre mente e cérebro.

Uma analogia melhor, talvez mais adequada para a era moderna, pode-se encontrar nos conceitos de hardware e software na informática. Num computador, o hardware desempenha o papel do cérebro, embora o software é análogo à mente. Podemos aceitar com agrado que o resultado proporcionado por um computador está rigorosamente determinado em sua totalidade pelas leis dos circuitos elétricos mais os dados de entrada utilizados. Raramente perguntamos "como se regula o programa para fazer que todos esses pequenos circuitos disparem-se de acordo com a seqüência correta?" Não obstante, sentimo-nos contentes em dar uma descrição equivalente em linguagem de software, usando conceitos como input, output, cálculo, dados, respostas, etc.

As descrições gêmeas de hardware e software aplicadas à operação dos computadores são mutuamente complementares, não contraditórias. A situação tem, portanto, um estreito paralelismo com o princípio de complementariedade de Bohr. Certamente, a analogia é muito estreita quando consideramos a questão da dualidade onda-partícula. Como temos visto, uma onda quântica é realmente uma descrição de nosso CONHECIMENTO do sistema (quer dizer, um conceito de software), embora uma partícula é uma peça de hardware. O paradoxo da mecânica quântica é que, de certo modo, os níveis de descrição de hardware e software tem chegado a entrelaçar-se inextrincavelmente. Parece que não entendemos o espírito no átomo até que cheguemos a entender o espírito na máquina.

A INTERPRETAÇÃO DOS MUITO-UNIVERSOS

Tanto quanto se trata com um sistema finito resulta possível ignorar os problemas associados com o processo de medida quântica. Pode-se sempre contar com a interação com o meio para colapsar a função de onda. Esta linha de raciocínio falha completamente, entretanto, quando consideramos o tema da cosmologia quântica. Se aplicamos a mecânica quântica ao universo em sua totalidade, a noção de um aparelho de medida externo não tem sentido. Salvo que se envolve de algum modo à mente, o físico que deseja dar sentido à cosmologia quântica parece ser forçado a encontrar um significado ao ato de medida a partir dos próprios estados quânticos, pois não é neste caso possível que um instrumento de medida externo realize o colapso irreversível das funções de onda.

O interesse na cosmologia quântica cresceu nos anos 60, com o descobrimento de um certo número de teoremas em relação com as singularidades espaço-temporais. Estas são como fronteiras ou bordas do espaço-tempo nas quais se extingue a física conhecida. As singularidades se formam a partir de campos gravitacionais intensos e se supõe que existam dentro de buracos negros. Acredita-se também que o universo começou com uma singularidade. Posto que as singularidades representam o colapso total da física, alguns físicos as consideram patologias desagradáveis. Suspeitam que as singularidades podem ser um artifício de nosso incompleto estado de conhecimento acerca da gravidade, que na atualidade é incapaz de incorporar os efeitos quânticos satisfatoriamente. Tem-se argumentado que se os efeitos quânticos pudessem ser tomados em conta as singularidades desapareceriam. Para suprimir a singularidade big-bang temos de dar sentido à cosmologia quântica.

Em 1957 Hugh Everett propôs uma interpretação da mecânica quântica radicalmente distinta que elimina os obstáculos conceituais da cosmologia quântica. Recorde-se que a essência do problema quântico da medida radica em compreender como um sistema quântico que se encontra em uma superposição de, digamos, dois ou mais estados salta bruscamente a um estado particular com um observável bem definido como resultado de uma medida (Fig 10). Um bom exemplo é o experimento do gato de Schrödinger discutido na página 45. Nesse caso o sistema quântico pode desenvolver-se em dois estados muito diferentes: gato vivo e gato morto. Em conseqüência, as idéias mecânico - quânticas não logram explicar como a superposição gato vivo - gato morto se converte na alternativa ora morto ora vivo.

Segundo Everett a transição tem lugar porque o universo se divide em duas cópias, uma que contém um gato vivo e a outra um gato morto. Ambos universos contém também uma cópia do experimentador, cada um dos quais acredita que é o único. Em geral, se um sistema quântico encontra-se em uma superposição de, digamos, n estados quânticos, então após a medida o universo se dividirá em n cópias. Na maioria dos casos, n é infinito. Daí que devemos aceitar que há realmente uma infinidade de "mundos paralelos" coexistindo com o que vemos em cada instante. Ademais, há uma infinidade de indivíduos mais ou menos idênticos a nós habitando esses mundos. É uma idéia certamente rara.

Na versão original da teoria supunha-se que o universo se bifurca cada vez que tem lugar uma medida, ainda que permanecia sempre vago o que constituía exatamente uma medida. Algumas vezes usava-se o termo "interação tipo-medida", e parece como se a bifurcação pudesse ocorrer inclusive a partir dos "saltos" normais de átomos observados. Um proponente da interpretação dos muitos universos, Bryce De Witt, a descreve do modo seguinte:

Qualquer transição quântica que tenha lugar em qualquer estrela, em qualquer galáxia, em qualquer esquina remota do universo, divide nosso mundo local terrestre em miríades de cópias de si mesmo....Eis aqui esquizofrenia a vontade.

Mais recentemente David Deutsch (veja o capítulo 6) modificou ligeiramente a teoria, de modo que o número de universos permanece fixo, não há bifurcação. No lugar dele , a maioria dos universos são em princípio completamente idênticos.

Quando tem lugar uma medida, aparece a diferenciação. Assim, no experimento do gato de Schrödinger dois universos idênticos previamente diferenciam-se, de modo que num deles o gato permanece vivo embora no outro morre. Uma vantagem desta nova imagem é que evita a enganosa impressão de que acontece algo mecânico como parecia ser o caso se o universo se bifurcasse realmente.

Duas importantes críticas tem-se levantado contra a teoria dos muitos universos. A primeira é que introduz uma quantidade absurda de "equipamento metafísico em excesso" na nossa descrição do mundo físico. Somente experimentamos nosso universo, assim que introduzir uma infinidade de outros simplesmente para explicar uma sutileza técnica (o colapso da função de onda) que ocorre no nosso parece ser a antítese da Navalha de Occam.

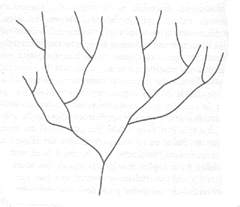
Fig. 10 - O universo em ramificação. Segundo Everett, quando a um sistema quântico é apresentado uma escolha entre vários resultados possíveis, o universo se fragmenta de modo que todos eles dão-se em realidade. Isto implica que qualquer universo dado está se fragmentando continuamente em um fantástico número de universos parecidos.

Em sua defesa, os proponentes da teoria argumentam que o "hardware" teórico é menos relevante numa teoria que o número de suposições fundamentais que se fazem ao formulá-la. O resto das interpretações da mecânica quântica introduz alguma classe de hipótese epistemológica para dar sentido ao que a primeira vista é uma teoria sem sentido. Entretanto, a teoria dos muitos universos não tem necessidade disto. A interpretação, assegura-se, surge automaticamente das regras formais da mecânica quântica, sem necessidade de nenhum tipo de suposição acerca do que a teoria significa. Não é necessária a introdução de um postulado aparte segundo o qual, após uma medida, a função de onda colapsa. Por definição, cada universo alternativo contém uma de cada das possíveis funções de onda colapsadas.

A segunda objeção à teoria é que se a considera inverificável. Se nossa consciência está confinada num universo em cada momento, como poderíamos sequer confirmar ou refutar a existência dos demais? Como veremos, resulta notável que a teoria possa, depois de tudo, ser comprovada, se estivermos disposto a aceitar a possibilidade de computadores inteligentes.

Um argumento final a favor da existência de um conjunto completo de universos é que isto proporcionaria uma explicação fácil a uma grande quantidade de "coincidências" misteriosas e "acidentes da natureza" que se encontram na física, na biologia e na cosmologia. Por exemplo resulta que, a grande escala, o universo está ordenado de um modo notável, com a matéria e a energia distribuída de forma altamente improvável. É difícil explicar como tão fortuita disposição tenha podido surgir do caos aleatório do big-bang. Se a teoria dos muitos universos for, entretanto, correta, a aparente pré-fabricada organização do cosmo não seria um mistério. Poderíamos supor sem risco que todas as disposições possíveis de matéria e energia acham-se representadas em algum lugar dentre os infinitos universos. Somente em uma proporção diminuta do total as coisas se disporiam do modo preciso para que aparecessem organismos vivos e, em conseqüência, observadores. Assim, pois, somente é essa fração atípica a que se observa em qualquer caso. Em breve, nosso universo é destacável porque o temos selecionado a causa de nossa própria existência!!

A INTERPRETAÇÃO ESTATÍSTICA

Nesta maneira de ver as coisas, o físico abandona qualquer intento de descobrir o que se sucede realmente num sucesso de medida quântica e se fixa, pelo contrário, a afirmações sobre conjuntos completos de medidas. A mecânica quântica prediz corretamente as probabilidades dos resultados possíveis de uma medida, e no entanto se restringe a atenção à estatística global, não há questão alguma que responder no que se refere ao problema da medida.

Poderia objetar-se que a interpretação estatística ( ou de conjuntos) não resolve o problema da medida, senão simplesmente o põe de lado. O preço que se paga é que não há esperança alguma de discutir o que ocorre realmente quando uma medida individual acontece.

O POTENCIAL QUÂNTICO

Um tratamento inteiramente diferente tem-se desenvolvido a partir das tentativas de se construir uma teoria de variáveis ocultas da mecânica quântica. Como se discutiu na página 17, a mecânica quântica prediz que a desigualdade de Bell viola-se. Se isto é correto, é necessário renunciar a uma das hipóteses físicas que se fizeram para prová-la. Uma delas é "realidade". Como temos visto, a interpretação de Copenhagem de Bohr adota esta postura. A outra hipótese é a de "localidade": em termos não muito precisos, inexistência de propagação de efeitos físicos a velocidade maior que a da luz.

Se se abandona a localidade, resulta possível reinventar uma descrição do micromundo muito semelhante à do mundo cotidiano, com objetos que gozam de uma existência independente em estados bem definidos e possuem conjuntos completos de atributos físicos. Não há necessidade de borrosidade nesse caso.

O preço a pagar é, desde logo, que os efeitos não locais aportam sua própria colheita de dificuldades; especificamente, a capacidade para que certos sinais viajem até o passado. Isto abriria o caminho a todo tipo de paradoxos causais.

Apesar destas dificuldades, alguns pesquisadores, David Bohm e Basil Hiley de modo muito notável (veja os capítulos 8 e 9), prosseguiram com a idéia de uma teoria de variáveis ocultas não locais, inventando o que eles chamaram de "potencial quântico". Este é semelhante aos potenciais mais familiares associados com campos de força tais como a gravidade ou o eletromagnetismo, mas difere deles em que a atividade do potencial quântico depende da estrutura holística do sistema. Isto é leva informação acerca do aparelho de medida, de observadores distantes e assim sucessivamente. Em conseqüência, a situação física completa em uma região ampla do espaço (em princípio o universo em sua totalidade) fica englobada neste potencial.

Apesar dos extenuadores esforços para dar sentido à física quântica, não há ainda acordo entre os físicos acerca do método que deva se adotar. Certamente o breve resumo exposto mais acima não esgota de nenhuma maneira o espectro completo das diferentes interpretações que tem sido discutidas em anos recentes. É verdadeiramente notável que uma teoria que de outro modo era mais ou menos completa em seus detalhes essenciais faça meio século e que resultou espetacularmente cheia de êxito em aplicações práticas, permaneça, entretanto, sem acabar. Este estado de coisas é devido em grande parte a que as discussões sobre os fundamentos da mecânica quântica são mormente teóricos. No máximo tendem a envolver "experimento ideais". A região de interesse é tão difícil de explorar que resulta muito raro que possam ser realizados experimentos práticos para verificar os fundamentos da teoria. Por esta razão, o teste experimental da desigualdade de Bell efetuado por Aspect e colaboradores foi recebido com um interesse científico enorme.

BIBLIOGRAFIA

T. Bastin (ed.), Quantum Theory and Beyond (Cambridge University Press, Cambridge, 1971).
D. Bohm, Wholeness and the Implicate Order (Routledge & Kegan Paul, Londres, 1980).
J. F. Clauser e A. Shimony, « Bell's theorem: experimental tests and implications» , em Reports on Progress in Physics 41, 1881-1927 (1978).
B. D'Espagnat, The Conceptual Foundations of Quantum Mechanics (Benjamin, Nova York, 1971; In Search of Reality (Springer-Verlag, Nova York, 1983) (Edição espanhola: En busca de lo real, Alianza Universidad, Madrid, 1983); « Quantum Theory and Reality» em Scientific American, novembro 1979, 158-181 (edição espanhola: Investigación y Ciencia, janeiro 1980, 80-95).
B. S. De Witt, « Quantum Mechanics and Reality» , em Physics Today, setembro 1970,30-35.
B. S. De Witt e N. Graham, The Many-Worlds Interpretation of Quantum Mechanics (Princeton University Press, Princeton, N.J., 1973).
W. Heisenberg, Physics and Philosophy (Harper & Row, Nova York, 1959).
M. Jammer, The Philosophy of Quantum Mechanics (John Wiley, Nova York, 1974).
N. D. Mermin, « Is the moon there when nobody looks? Reality and the quantum theory» , em Physics Today, abril 1985, 38-47.
A. I. M. Rae, Quantum Physics: Ilusion or Reality (Cambridge University Press, 1986). «Física Quántica: ¿Ilusión o realidad?» Alianza Universidad, Madrid, 1988.
G. Ryle, The Concept of Mind (Barnes & Noble, Londres, 1949).
J. von Neumann, Mathematical Foundations of Quantum Mechanics (Princeton University Press, Princeton, N.J., 1955).
J. A. Wheeler e W. H. Zurek, Quantum Theory and Measurement (Princeton University Press, Princeton, N.J., 1983).
E. P. Wigner, « Remarks on the mind-body question» , em The Scientist Speculates-An Antology of Partly-Baked Ideas, ed. I. J. Good, 284-302 (Basic Books, Nova York, 1962).