GABARITO DOS EXERCÍCIOS
PROPOSTOS
FATOR DE ACUMULAÇÃO DE CAPITAL
SÉRIE UNIFORME
SOLUÇÃO
R = R$
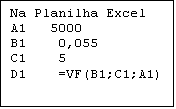
5.000,00 i = 5,5% a.m. n= 5 S
= ?
S = R [{(1 +
i)n - 1}/i] Þ S =
5.000 [{(1 + 0.055)5 - 1}/0.055]
S = 5.000
[{(1.055)5 - 1}/0.055] = 5.000 [{1.306960 - 1}/0.055]
S = 5.000
[0.306960/0.055] = 5.000 [5,581091] = 27.905,46
S
= 27.905,46
Pela HP 12-C, temos:
|
f
FIN f 2 5000
CHS PMT 5.5
i 5
n FV |
SOLUÇÃO
R = R$ 100,00 n = 5 meses i = 2%
a.m. S = ?
S = R [{(1 + i)n - 1}/i] Þ
S = 100 [{(1 + 0.02)5 - 1}/0.02]
S = 100 [{(1.02)5 - 1}/0.02]
= 100 [{1.104081 - 1}/0.02]
S = 100 [0.104081/0.02] = 100 [
5.204040] = 520.40
S
= R$ 520.40
Na Planilha Excel A1 100 B1 0,02 C1 5 D1 =VF(B1;C1;A1)
f FIN
f 2 100
CHS PMT 5 n 2 i FV |
SOLUÇÃO
R = 800,00 i = 0.5% = 0.005 a.m. n = 12 meses S = ?
S = R [{(1 + i)n - 1}/i] Þ
S = 800 [{(1 + 0.005)12 - 1}/0.005]
S = 800 [{(1.005)12 -
1}/0.005] Þ S = 800 [{1.061678 - 1}/0.005]
S = 800 [0.061678/0.005] Þ S = 800 [12.335562] = 9.868,45
|
f FIN f
2 800 CHS PMT 12 n 0.5 i FV |
Na Planilha Excel A1 800 B1 0,005 C1 12 D1 =VF(B1;C1;A1)
SOLUÇÃO
R = ? i
= 6% a.a. n = 10 S = 400.000,00
S = R [{(1 + i)n - 1}/i] Þ
400.000 = R [{(1.06)10 - 1}/0.06]
400.000 = R [{1.790848 - 1}/0.06] Þ
400.000 = R [0.790848/0.06]
400.000 = R [13.180795] Þ
R = 400.000/13.180795
R
= 30.347,18

Na planilha Excel, para calcular o PGTO, devemos conhecer o
VP. Para tanto, criamos uma célula com a função VP para pagamentos simples, e
depois outra com a função PGTO. Assim,
SOLUÇÃO
R = ? n
= 6 anos S = 200.000,00 i = 25% = 0.25 a.a.
S = R [{(1 + i)n - 1}/i] Þ 200.000 = R [{(1.25)6 -1}/0.25]
200.000 = R [{2.814697}/0.25] Þ R = 200.000/11.258788 = 17.763,90
Na planilha excel adotar o mesmo
procedimento que o exercício 4, isto é, calcular o VP antes.
SOLUÇÃO
R = 8.093,00 S = 135.000,00 n = 15 i = ?
S = R [{(1 + i)n - 1}/i] Þ
135.000 = 8.093 S15ùi
S15ùi = ![]() = 16.681082
= 16.681082
Adotando o mesmo procedimento
do exercício 2 feito em classe, temos:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1% 16.096896
1% 16.096896
![]()
![]() i 16.681082
i 16.681082
![]()
![]() 2% 17.293417
2% 17.293417
![]() Þ i - 1 =
0.488235
Þ i - 1 =
0.488235
i = 1.488235 i
= 1,50% a.m.
Impossível de fazer no Excel
pois não conhecemos, e nem temos como calcular o VP.
MAIS
EXERCÍCIOS sobre FATOR DE ACUMULAÇÃO DE CAPITAL
7 . Qual é o depósito
trimestral durante 4 anos consecutivos que produz o montante de R$ 200.000,00
após o último depósito? Considerar as taxas de juros trimestrais a seguir:
a. 5% a.t. b. 10% a.t. c. 15% a.t.
SOLUÇÃO
n = 4 S
= 200.000 i = 5% a.t. R = ?
S = R [ {(1 + i)n - 1}/ i ] Þ
200.000 = R [{1 + 0.05)16 - 1}/0.05] =
= R [23,657492]
R = 200.000/23.657492 = R$ 8.453,98 \ R = R$ 8.453,98
Com a taxa i = 10% a.t., temos
S = R [ {(1 + i)n - 1}/ i ] Þ
200.000 = R [{1 + 0.10)16 - 1}/0.10] =
= R [ 35.949730]
R = 200.000/35.949730 = R$ 5.563,32 \
R = R$ 5.563,32
Com a taxa i = 15% a.t., temos
S = R [ {(1 + i)n - 1}/ i ] Þ
200.000 = R [{1 + 0.15)16 - 1}/0.15] =
= R [ 55.717472]
R = 200.000/55.717472 = R$ 3.589,54 \
R = R$ 3.589,54
Esses cálculos na calculadora
HP 12-C ficam:
|
f
FIN f 2 4
ENTER 4 x n 200000 CHS
FV 5
i PMT |
|
10
i PMT |
|
15
i PMT |
8. O pai de um
estudante efetua mensalmente, durante 36 meses, depósitos de R$ 200,00 em um
banco que paga 2% a.m., sobre o saldo credor. Este dinheiro se destina ao
custeamento dos estudos superiores do filho. Qual será o montante acumulado
após ser efetuado o último depósito?
SOLUÇÃO
R = R$ 200,00 i = 2% a.m. n = 36
meses S = ?
S = R [ {(1 + i)n - 1}/ i ] Þ
S = 200 [{1 + 0.02)36 -1}/0.02] =
= 200 [51.994367] = R$ 10.398,87
9. Uma pessoa,
planejando a construção de uma casa, prevê dispêndios mensais de R$ 100.000,00
nos meses de setembro, outubro e novembro. Quanto deve ser depositado
mensalmente de janeiro a agosto, do mesmo ano, para que seja possível efetuar
tais retiradas? Considerar remuneração de 3% a.m. sobre os depósitos.
SOLUÇÃO
![]()
![]()
![]() Temos o
seguinte problema: 100.000 100.000
100.000
Temos o
seguinte problema: 100.000 100.000
100.000
JAN FEV MAR
ABR MAI JUN JUL
AGO
![]()
SET
OUT NOV
R R
R R R R R
R
Portanto, o montante dos 8 depósitos
deve ser igual ao valor atual das 3 retiradas, à taxa de 3% a.m.
S = R1 [ {(1
+ i)n - 1}/ i ]
P = R2 [![]() ]
]
Como
S = P Þ R1 [ {(1 + i)n -
1}/ i ] = R2 [![]() ] ou
] ou
R1 [8.892336] = R2
[2,8286611 Þ R1 = (100.000
[2,8286611])/8,892336 R1 = R$
31.809,54
|
f
FIN f 2 100.000
CHS PMT 3
i 3
n PV f FIN CHS FV 8 n 3
i PMT |
Limpa os registros
financeiros e coloca duas casas decimais
Coloca as prestações iguais a
R$ 100.000,00
Taxa de juros igual a 3%
Número de períodos igual a 3
Valor atual dos desembolsos
Limpa novamente os registros
financeiros
Coloca o valor futuro da
série
Coloca o número de períodos
de aplicações
Coloca a taxa de 3% novamente
(foi apagada)
Calcula as prestações
10. A Imobiliária
Cabanas S/A vende um pequeno apartamento usado por R$ 150.000,00 a vista. Como
alternativasa seus clientes, oferece dois planos de financiamento:
|
Plano A : entrada de R$
50.000,00 mais 4 prestações trimestrais de R$ 31.600,00 Plano B : entrada de R$
30.000,00 mais 8 prestações trimestrais de R$ 23.000,00 |
O Sr. Malba Tahan da Silva, capitalista que aplica seu
dinheiro a 10% a.t., deseja saber qual é a melhor opção de compra.
SOLUÇÃO
Vamos calcular o valor atual de cada
plano, lembrando que no pagamento à vista o valor atual é o próprio valor.
Plano A: PV = Entrada1 + R1 [![]() ]=
]=
=
50.000 + 31.600 [![]() ] = 50.000 + 31.600 [3.169865]=
] = 50.000 + 31.600 [3.169865]=
=
R$ 150.167,75
Plano B: PV = Entrada2 + R2 [![]() ] =
] =
= 30.000 + 23.000 [![]() ] = 30.000 + 23.000 [5.334926]=
] = 30.000 + 23.000 [5.334926]=
=
R$ 152.703,30
Como nos dois planos de financiamento o
valor atual é superior ao preço a vista (R$ 150.000,00), então a melhor opção
de compra é a vista.
FATOR DE VALOR ATUAL
Série Uniforme
1. Qual é o valor da prestação mensal de um financiamento de
R$ 3.500,00, feito à base de 2% a.m. em 10 prestações? Resp:- R$ 389,64
Solução
P
= 3.500,00 i = 2% n = 10
P
= R . a10ù2
Þ R = 3.500 . ![]() = (3.500 .
0,11132653) = 389,64
= (3.500 .
0,11132653) = 389,64
O
valor da prestação mensal é de R$ 389,64
2. Pagando 20 prestações de R$ 300,00 num financiamento feito à base de
6% a.m., que dívida estarei amortizando?
Resp: R$ 3.440,97
Solução
R$ 300,00 i = 6% n
= 20
P = R . a20ù6
= 300 . 11,469921 = R$ 3.440,97
3. Em quantas prestações mensais
de R$ 796,80 quitarei uma dívida de R$ 10.000,00, se o financiamento foi feito
à base de 4% a.m.? Resp: 18 prestações
Solução
P = 10.000,00 R
= 796,80 i = 4%
P = R . anù4
10.000 = 796,80 . anù4
Þ anù4
= 12,550201
Procurando i = 4 nas Tabelas de anùi,
encontraremos em n =18 o fator 12,659270, que aceitaremos como o mais próximo.
Portanto, deverá ser 18 o número de prestações
mensais iguais.
4. Um financiamento de R$ 11.000,00 tem duas opções parra ser feito: em
12 prestações de R$ 1.384,92 ou em 18 prestações de R$ 1.015,92. Qual é a opção
mais vantajosa para a financiadora?Resp:- Para a financiadora é a primeira opção,
pois a taxa é maior
Solução
Na primeira opção, temos P = 11.000,00, R = 1.384,92 n = 12
P = R . a12ùi 11.000 = 1.384,92 . a12ùi
a12ùi
= (11.000/1.384,92) = 7,942697
Procurando n = 12 nas Tabelas de anùi,
encontraremos para i = 7 o valor 7,942686, que consideraremos o mais
aproximado. Assim, a taxa no primeiro caso é de, aproximadamente, 7% a.m.
Na segunda opção, temos P = 11.000,00 R = 1.015,92 n = 18
P = R . a18ùi
11.000 = 1.015,92 . a18ùi
a18ùi
= (11.000/1.015,92) = 10,827624
Procurando n = 18 nas Tabelas de anùi,
encontraremos para i = 6%, o fator 10,827603, que consideraremos o mais
aproximado. Assim, a taxa no segundo caso foi de 6% a.m., aproximadamente.
Para a financiadora é mais vantajosa a
primeira opção, pois a taxa é maior.
5. Calcular o valor atual de uma dívida de 8 termos iguais a
R$ 800,00, sendo a taxa no período de 2%. Resp: R$ 5.860,38
Solução
R = 800,00 i = 2% n = 8
P = R
. a8ù2
= 800 . 7,3254814 = 5.860,38 \ P = R$ 5.860,38
6. Um comprador oferece ao vendedor de uma loja 6 prestações de
R$ 429,00 por uma televisão, cujo preço à vista é de R$ 2.000,00. Só que ele
deseja começar a pagar daqui a 3 meses. Se os juros mensais normais da loja
forem de 3%, será ou não interessante para o vendedor aceitar a proposta? Resp: É vantajoso pois
o comprador está pagando um juro de R$
126,70 a mais do que se financiasse pela loja.
Solução
P = 2.000,00 R =
429,00
P = R [a9ùi
- a3ùi]
= 3.340,20 - 1213,50 = 2.126,70
O comprador está pagando R$ 126,70 a mais do
que se o financiamento fosse feito pela loja.
Solução
R = R$ 1.846,30 i = 5% a.m. carência
= 2 meses
número de
parcelas = 6
Valor
Financiado (V.F.) = P - 0.15 P = 0.85 P
0.85 P
= R [a8ù5
- a2ù5
] = 1.846,30 [ 6,4632128 - 1,8594104]
0.86 P
= 1.846,30 [4,6038024] = 8.500,00 \
P = R$ 10.000,00
Solução
Calculando o valor das prestações mensais:
P = 20.000,00 n
= 8 i = 8% comissão = ?
P = R . a8ù8
20.000 = R . 5,74664 R = R$ 3.480,29
O valor atual das 8 prestações de R$ 3.480,29,
à taxa de juros de 10%a.m.:
P = R . a8ù10
= 3.480,29 . 5,33493 = 18.566,62
Valor da Comissão:
Comissão = 20.000 - 18.566,62 = R$ 1.433,38
Solução
n =18 R = 100.000,00 P
= 875.563,00 i = ?
P = R
. a18ùi
a18ùi
= (875.563/100.000) = 8,75563
Procurando nas Tabelas Financeiras o fator a18ùi
= 8,75563 vemos que corresponde a uma taxa de juros de 9% a.m.. Se o fator não
estiver tabelado, podemos usar o método da interpolação linear.
10.Uma pessoa deseja comprar um microcomputador. Dispõe de 4
alternativas para pagamento:
1. pagamento à vista de R$ 2.300,00;
2. pagamento de 8 prestações mensais
de R$ 431,11;
3. Pagamento de 4 prestações mensais
de R$ 965,75 sendo a primeira paga
daqui a 4 meses;
4. Um único pagamento de R$ 4.930,26
daqui a 8 meses.
Do ponto de vista financeiro, qual plano é
o melhor considerando que a taxa de juros praticada é de 10% a.m.? Resp: Todas alternativas são equivalentes.
Solução
Os valores atuais dos 4 planos de
financiamento são os seguintes:
1. P = R$ 2.300
2. P = 431,12 . a8ù10
= 431,12 . 5,33493 = 2.300,00
3. P = [ 965,75 . a4ù10
] (1,10)-3 = 965,75 . 3,16987 . 0,75131 = R$2.300
4. 4.930,26 . (1,10)-8
= 4.930,26 . 0,46651 = R$ 2.300,00
Observando os resultados, vemos que as
quatro alternativas são equivalentes, considerada a taxa de 10% a.m.
FATOR DE FORMAÇÃO DO CAPITAL
SÉRIE UNIFORME
1.
Uma financeira publica que seus coeficientes para
financiamento de carros, em 24 meses, são:
Carros 0 - km Carros Novos
0,06480 0,06815
Qual é a taxa de juros de cada coeficiente?Resp : Carros-Novos
3,88% a.m. e Carros-Usados 4,38% a.m.
Solução
O coeficiente é o número que multiplicado pelo valor à vista P do
carro dá o valor das prestações, isto é,
0,06480 x P = R Þ P = R / 0,06840 Þ P = R . 15,43.
Mas, P = R a24ùi. Logo,
a24ùi = 15,43
Fazendo interpolação linear, teremos:
i = 3%
...............16,9130
i.....................15,43
i = 4%
...............15,2469
![]()
i - 3 = 0,88 ou i = 3,88% a.m.
Obs: - Para os carros usados adotamos o mesmo raciocínio.
Solução
P = 30.000,00 R = 1.326,06 i = 4% a.m. n =?
P = R anù4 30.000 = 1.326,06 . anù4
anù4 = 22,6234 Þ ![]() = 22,6234 Þ 1 - (1.04)-n
= 0,9049
= 22,6234 Þ 1 - (1.04)-n
= 0,9049
-n ln 1.04 = ln 0.0951 Þ -n = (-2.3528263/0.0392207) = 59.99
n = 60 meses
Solução
500.000,00
![]()
![]()
![]()
![]()
![]()
![]()
0 1 2 3
4 5 47 48

![]()
1 2 3
4 5 6
R
R R R R R
R
O valor futuro da série de depósitos de ve ser igual ao
valor presente da série de retiradas,
com carência de 2 anos. Assim,
S = R s48ù2,5 = P6 - P1
= 500.000,00 (a6ùi - a1ùi).
Como a série de retirada é
anual, temos:
(1 + ia.a.) = (1 + i)12 Þ 1 + ia.a. =
1,344889 \
ia.a. = 34,4889% a.a.
R . s48ù2,5 = 1.204.738,457 - 371.777,8939 = 832.960,56
R . [((1.025)48
- 1)/.025] = 832.960,56
R = 9.167,56
FATOR
DE RECUPERAÇÃO DE CAPITAL
SÉRIE UNIFORME
1. Um jornal local
publicou o seguinte anúncio de uma revendedora de veículos:
“Gol 95. Novinho. Entr. R$ 4.500,00 e 12 parcelas mensais
de R$ 600,00; à vista R$ 9.600,00; temos outros planos; aceitamos outro veículo
em troca. Tel xxx-xxxx”
Qual a taxa de
juros que o vendedor cobra no caso de financiar o carro? Resp:- 5,75% ao mês